Question Number 5261 by Kasih last updated on 03/May/16
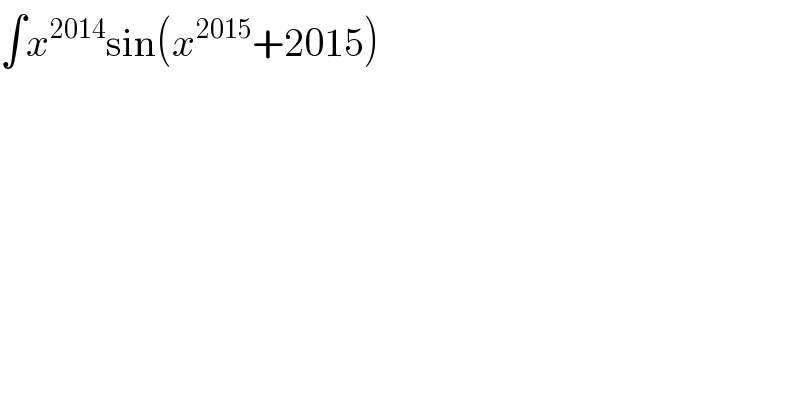
$$\int{x}^{\mathrm{2014}} \mathrm{sin}\left({x}^{\mathrm{2015}} +\mathrm{2015}\right) \\ $$
Answered by Yozzii last updated on 03/May/16
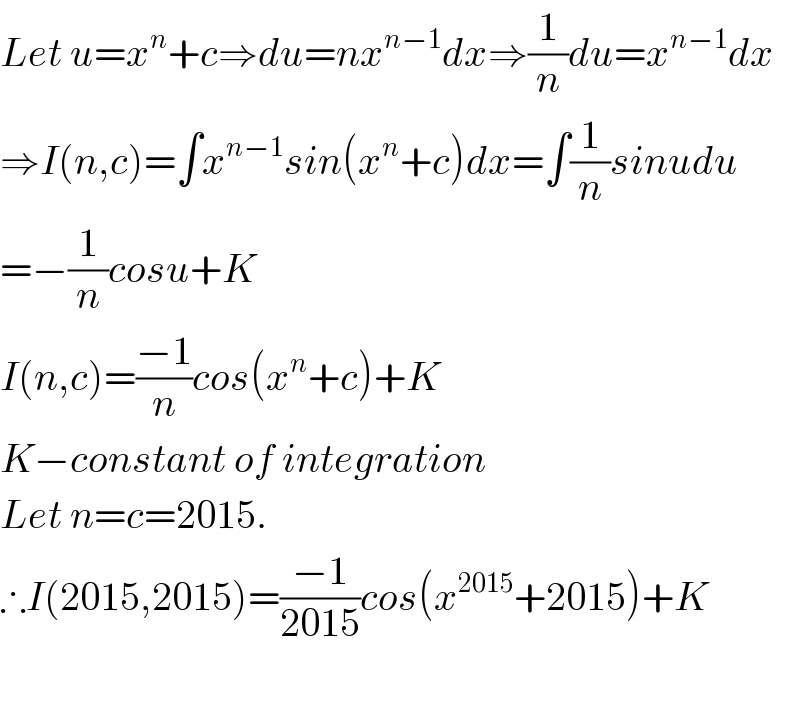
$${Let}\:{u}={x}^{{n}} +{c}\Rightarrow{du}={nx}^{{n}−\mathrm{1}} {dx}\Rightarrow\frac{\mathrm{1}}{{n}}{du}={x}^{{n}−\mathrm{1}} {dx} \\ $$$$\Rightarrow{I}\left({n},{c}\right)=\int{x}^{{n}−\mathrm{1}} {sin}\left({x}^{{n}} +{c}\right){dx}=\int\frac{\mathrm{1}}{{n}}{sinudu} \\ $$$$=−\frac{\mathrm{1}}{{n}}{cosu}+{K} \\ $$$${I}\left({n},{c}\right)=\frac{−\mathrm{1}}{{n}}{cos}\left({x}^{{n}} +{c}\right)+{K} \\ $$$${K}−{constant}\:{of}\:{integration} \\ $$$${Let}\:{n}={c}=\mathrm{2015}. \\ $$$$\therefore{I}\left(\mathrm{2015},\mathrm{2015}\right)=\frac{−\mathrm{1}}{\mathrm{2015}}{cos}\left({x}^{\mathrm{2015}} +\mathrm{2015}\right)+{K} \\ $$$$ \\ $$
