Question Number 142802 by Gbenga last updated on 05/Jun/21

$${x}=\mathrm{2}{w}\left({e}^{−\mathrm{1}} \right) \\ $$
Commented by Dwaipayan Shikari last updated on 06/Jun/21

$${W}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}{x}^{{n}} \\ $$$${x}=\frac{\mathrm{2}}{{e}}−\mathrm{2}\left(\frac{\mathrm{1}}{{e}}\right)^{\mathrm{2}} +\mathrm{3}\left(\frac{\mathrm{1}}{{e}}\right)^{\mathrm{3}} −.. \\ $$
Answered by MJS_new last updated on 06/Jun/21
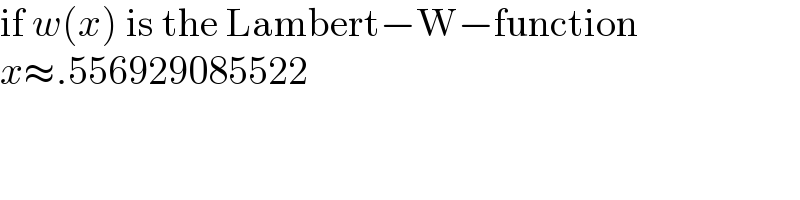
$$\mathrm{if}\:{w}\left({x}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{Lambert}−\mathrm{W}−\mathrm{function} \\ $$$${x}\approx.\mathrm{556929085522} \\ $$
