Question Number 10193 by konen last updated on 29/Jan/17
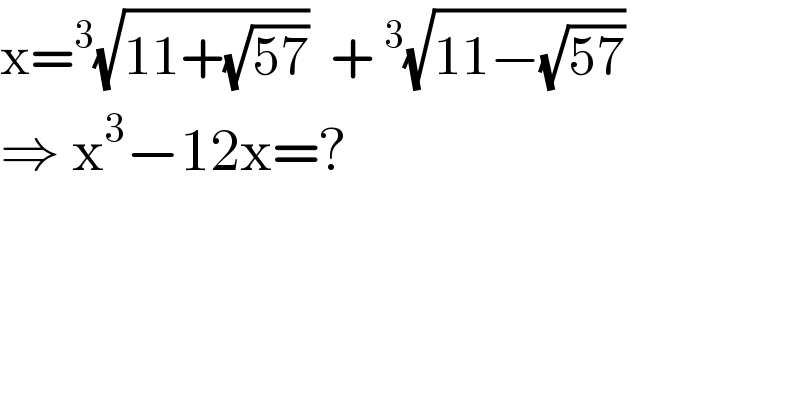
$$\mathrm{x}=^{\mathrm{3}} \sqrt{\mathrm{11}+\sqrt{\mathrm{57}}}\:\:+\:^{\mathrm{3}} \sqrt{\mathrm{11}−\sqrt{\mathrm{57}}} \\ $$$$\Rightarrow\:\mathrm{x}^{\mathrm{3}} −\mathrm{12x}=? \\ $$
Answered by ridwan balatif last updated on 29/Jan/17
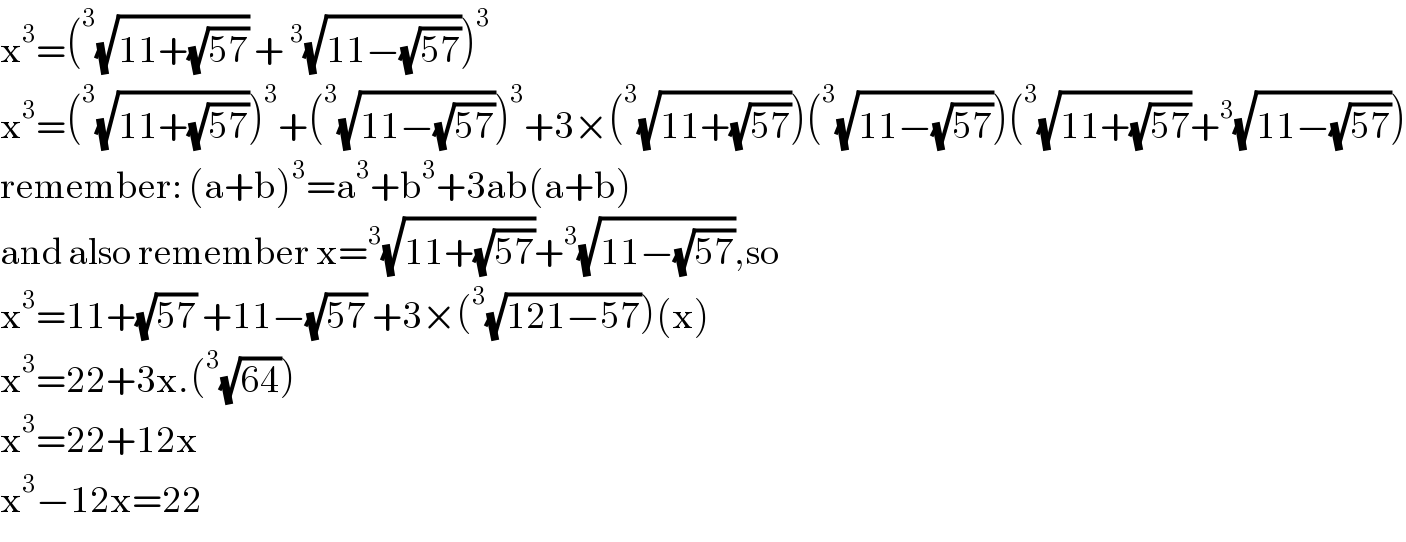
$$\mathrm{x}^{\mathrm{3}} =\left(^{\mathrm{3}} \sqrt{\mathrm{11}+\sqrt{\mathrm{57}}}\:+\:^{\mathrm{3}} \sqrt{\mathrm{11}−\sqrt{\mathrm{57}}}\right)^{\mathrm{3}} \\ $$$$\mathrm{x}^{\mathrm{3}} =\left(^{\mathrm{3}} \sqrt{\mathrm{11}+\sqrt{\mathrm{57}}}\right)^{\mathrm{3}} +\left(^{\mathrm{3}} \sqrt{\mathrm{11}−\sqrt{\mathrm{57}}}\right)^{\mathrm{3}} +\mathrm{3}×\left(^{\mathrm{3}} \sqrt{\mathrm{11}+\sqrt{\mathrm{57}}}\right)\left(^{\mathrm{3}} \sqrt{\mathrm{11}−\sqrt{\mathrm{57}}}\right)\left(^{\mathrm{3}} \sqrt{\mathrm{11}+\sqrt{\mathrm{57}}}+^{\mathrm{3}} \sqrt{\mathrm{11}−\sqrt{\mathrm{57}}}\right) \\ $$$$\mathrm{remember}:\:\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{3}} =\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{3ab}\left(\mathrm{a}+\mathrm{b}\right) \\ $$$$\mathrm{and}\:\mathrm{also}\:\mathrm{remember}\:\mathrm{x}=^{\mathrm{3}} \sqrt{\mathrm{11}+\sqrt{\mathrm{57}}}+^{\mathrm{3}} \sqrt{\mathrm{11}−\sqrt{\mathrm{57}}},\mathrm{so} \\ $$$$\mathrm{x}^{\mathrm{3}} =\mathrm{11}+\sqrt{\mathrm{57}}\:+\mathrm{11}−\sqrt{\mathrm{57}}\:+\mathrm{3}×\left(^{\mathrm{3}} \sqrt{\mathrm{121}−\mathrm{57}}\right)\left(\mathrm{x}\right) \\ $$$$\mathrm{x}^{\mathrm{3}} =\mathrm{22}+\mathrm{3x}.\left(^{\mathrm{3}} \sqrt{\mathrm{64}}\right) \\ $$$$\mathrm{x}^{\mathrm{3}} =\mathrm{22}+\mathrm{12x} \\ $$$$\mathrm{x}^{\mathrm{3}} −\mathrm{12x}=\mathrm{22} \\ $$
