Question Number 12968 by @ANTARES_VY last updated on 08/May/17

$$\left(\boldsymbol{\mathrm{x}}+\mathrm{3}\right)^{\mathrm{2}} +\left(\boldsymbol{\mathrm{y}}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{45}\:\:\:\boldsymbol{\mathrm{A}}\left(\mathrm{0};\mathrm{11}\right) \\ $$$$\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{circle}}\:\:\boldsymbol{\mathrm{to}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{point}}\:\:\boldsymbol{\mathrm{of}} \\ $$$$\boldsymbol{\mathrm{trying}}\:\:\boldsymbol{\mathrm{to}}\:\:\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{angular}}\:\:\boldsymbol{\mathrm{coefficient}}. \\ $$
Answered by 433 last updated on 08/May/17
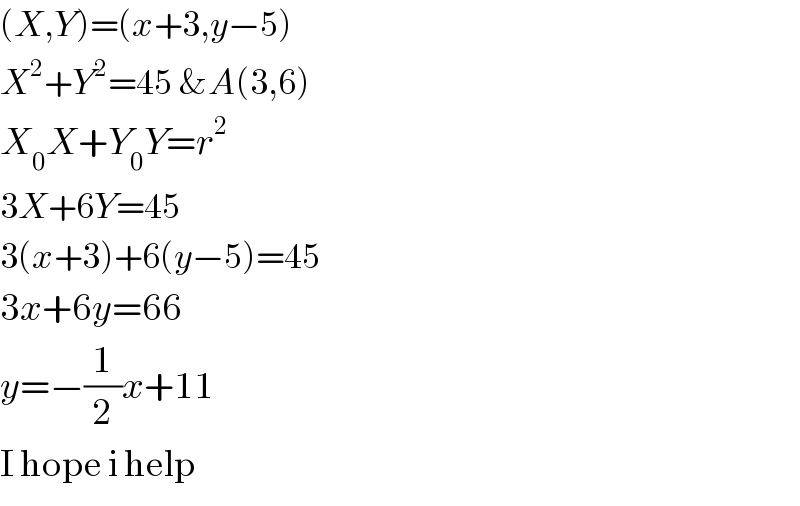
$$\left({X},{Y}\right)=\left({x}+\mathrm{3},{y}−\mathrm{5}\right) \\ $$$${X}^{\mathrm{2}} +{Y}^{\mathrm{2}} =\mathrm{45}\:\&{A}\left(\mathrm{3},\mathrm{6}\right) \\ $$$${X}_{\mathrm{0}} {X}+{Y}_{\mathrm{0}} {Y}={r}^{\mathrm{2}} \\ $$$$\mathrm{3}{X}+\mathrm{6}{Y}=\mathrm{45} \\ $$$$\mathrm{3}\left({x}+\mathrm{3}\right)+\mathrm{6}\left({y}−\mathrm{5}\right)=\mathrm{45} \\ $$$$\mathrm{3}{x}+\mathrm{6}{y}=\mathrm{66} \\ $$$${y}=−\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{11} \\ $$$$\mathrm{I}\:\mathrm{hope}\:\mathrm{i}\:\mathrm{help} \\ $$
