Question Number 74148 by mathocean1 last updated on 19/Nov/19
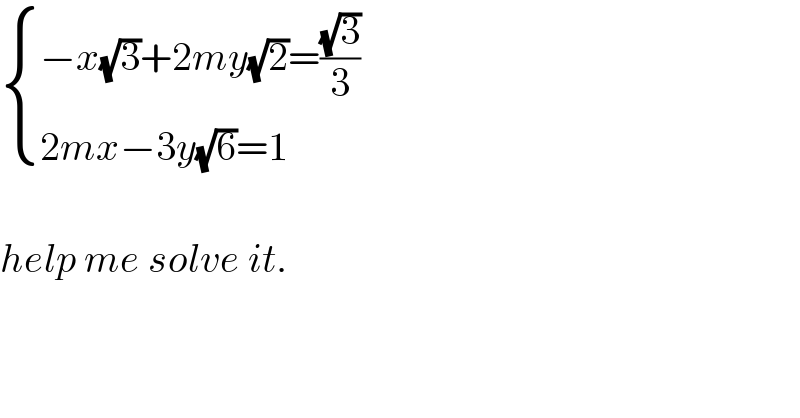
$$\begin{cases}{−{x}\sqrt{\mathrm{3}}+\mathrm{2}{my}\sqrt{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}}\\{\mathrm{2}{mx}−\mathrm{3}{y}\sqrt{\mathrm{6}}=\mathrm{1}}\end{cases}\:\:\:\:\:\: \\ $$$$ \\ $$$${help}\:{me}\:{solve}\:{it}. \\ $$
Answered by MJS last updated on 19/Nov/19

$$\mathrm{2}\:\mathrm{equations}\:\mathrm{in}\:\mathrm{3}\:\mathrm{unknowns}\:\Rightarrow\:\mathrm{parametric} \\ $$$$\mathrm{solution} \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow\:{y}=\frac{\sqrt{\mathrm{6}}}{\mathrm{12}{m}}\left(\mathrm{3}{x}+\mathrm{1}\right) \\ $$$$\left(\mathrm{2}\right)\:\Rightarrow\:{y}=\frac{\sqrt{\mathrm{6}}}{\mathrm{18}}\left(\mathrm{2}{mx}−\mathrm{1}\right) \\ $$$$\frac{\sqrt{\mathrm{6}}}{\mathrm{12}{m}}\left(\mathrm{3}{x}+\mathrm{1}\right)=\frac{\sqrt{\mathrm{6}}}{\mathrm{18}}\left(\mathrm{2}{mx}−\mathrm{1}\right) \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{1}}{\mathrm{2}{m}−\mathrm{3}}\:\Rightarrow\:{y}=\frac{\sqrt{\mathrm{6}}}{\mathrm{6}\left(\mathrm{2}{m}−\mathrm{3}\right)} \\ $$
