Question Number 10043 by konen last updated on 21/Jan/17
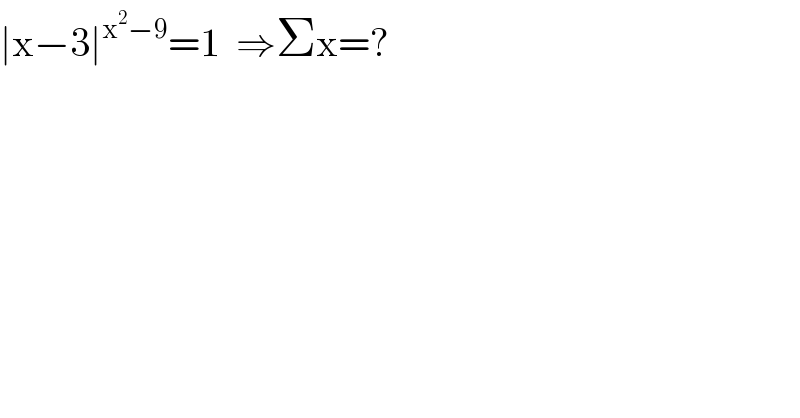
$$\mid\mathrm{x}−\mathrm{3}\mid^{\mathrm{x}^{\mathrm{2}} −\mathrm{9}} =\mathrm{1}\:\:\Rightarrow\Sigma\mathrm{x}=? \\ $$
Answered by mrW1 last updated on 22/Jan/17

$${if}\:{a}^{{b}} =\mathrm{1},\:{then} \\ $$$${a}=\mathrm{1}\:{or} \\ $$$${b}=\mathrm{0}\:{and}\:{a}\neq\mathrm{0} \\ $$$$ \\ $$$${since}\:\mid\mathrm{x}−\mathrm{3}\mid^{\mathrm{x}^{\mathrm{2}} −\mathrm{9}} =\mathrm{1} \\ $$$$\Rightarrow\mid{x}−\mathrm{3}\mid=\mathrm{1}\:\:\:\:\:…\left({i}\right) \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{9}=\mathrm{0}\:\:{and}\:{x}−\mathrm{3}\neq\mathrm{0}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right)\:\Rightarrow \\ $$$${x}−\mathrm{3}=\pm\mathrm{1} \\ $$$${x}=\pm\mathrm{1}+\mathrm{3} \\ $$$$\Rightarrow{x}=\mathrm{2}\:{or}\:\mathrm{4} \\ $$$$ \\ $$$${from}\:\left({ii}\right)\:\Rightarrow \\ $$$${x}^{\mathrm{2}} =\mathrm{9}\:{and}\:{x}\neq\mathrm{3} \\ $$$$\Rightarrow{x}=−\mathrm{3} \\ $$$$ \\ $$$${x}=\left(−\mathrm{3},\mathrm{2},\mathrm{4}\right) \\ $$$$\Sigma{x}=−\mathrm{3}+\mathrm{2}+\mathrm{4}=\mathrm{3} \\ $$
