x-3-x-2-9-dx-

Question Number 136301 by aurpeyz last updated on 20/Mar/21

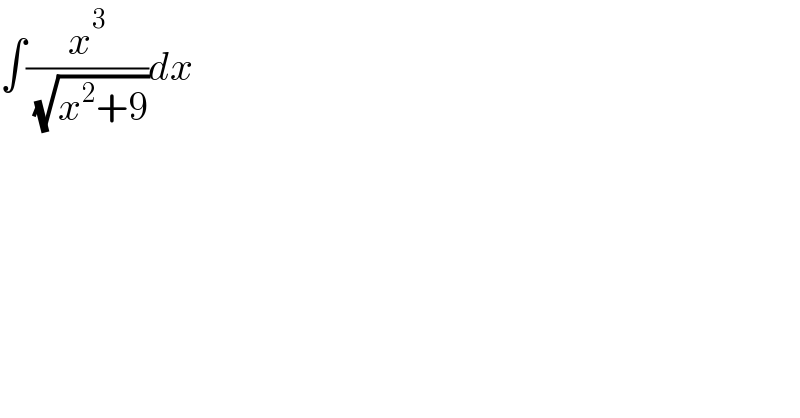
$$\int\frac{{x}^{\mathrm{3}} }{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}{dx} \\ $$

Answered by liberty last updated on 20/Mar/21

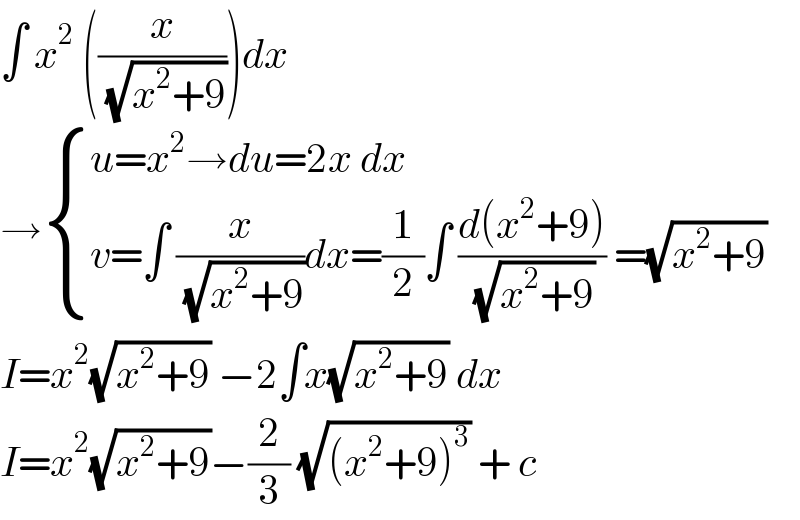
∫ x^2 ((x/( (√(x^2 +9)))))dx → { ((u=x^2 →du=2x dx)),((v=∫ (x/( (√(x^2 +9))))dx=(1/2)∫ ((d(x^2 +9))/( (√(x^2 +9)))) =(√(x^2 +9)))) :} I=x^2 (√(x^2 +9)) −2∫x(√(x^2 +9)) dx I=x^2 (√(x^2 +9))−(2/3) (√((x^2 +9)^3 )) + c

$$\int\:{x}^{\mathrm{2}} \:\left(\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}\right){dx} \\ $$$$\rightarrow\begin{cases}{{u}={x}^{\mathrm{2}} \rightarrow{du}=\mathrm{2}{x}\:{dx}}\\{{v}=\int\:\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{d}\left({x}^{\mathrm{2}} +\mathrm{9}\right)}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}\:=\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}\end{cases} \\ $$$${I}={x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +\mathrm{9}}\:−\mathrm{2}\int{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}\:{dx} \\ $$$${I}={x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +\mathrm{9}}−\frac{\mathrm{2}}{\mathrm{3}}\:\sqrt{\left({x}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{3}} }\:+\:{c} \\ $$

Commented by aurpeyz last updated on 20/Mar/21

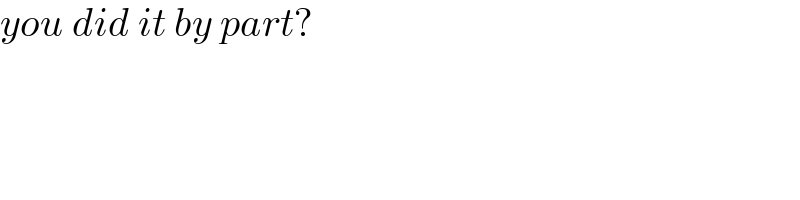
$${you}\:{did}\:{it}\:{by}\:{part}? \\ $$

Commented by liberty last updated on 20/Mar/21

$${yes} \\ $$

Commented by aurpeyz last updated on 20/Mar/21

$${thanks} \\ $$

Answered by mathmax by abdo last updated on 20/Mar/21

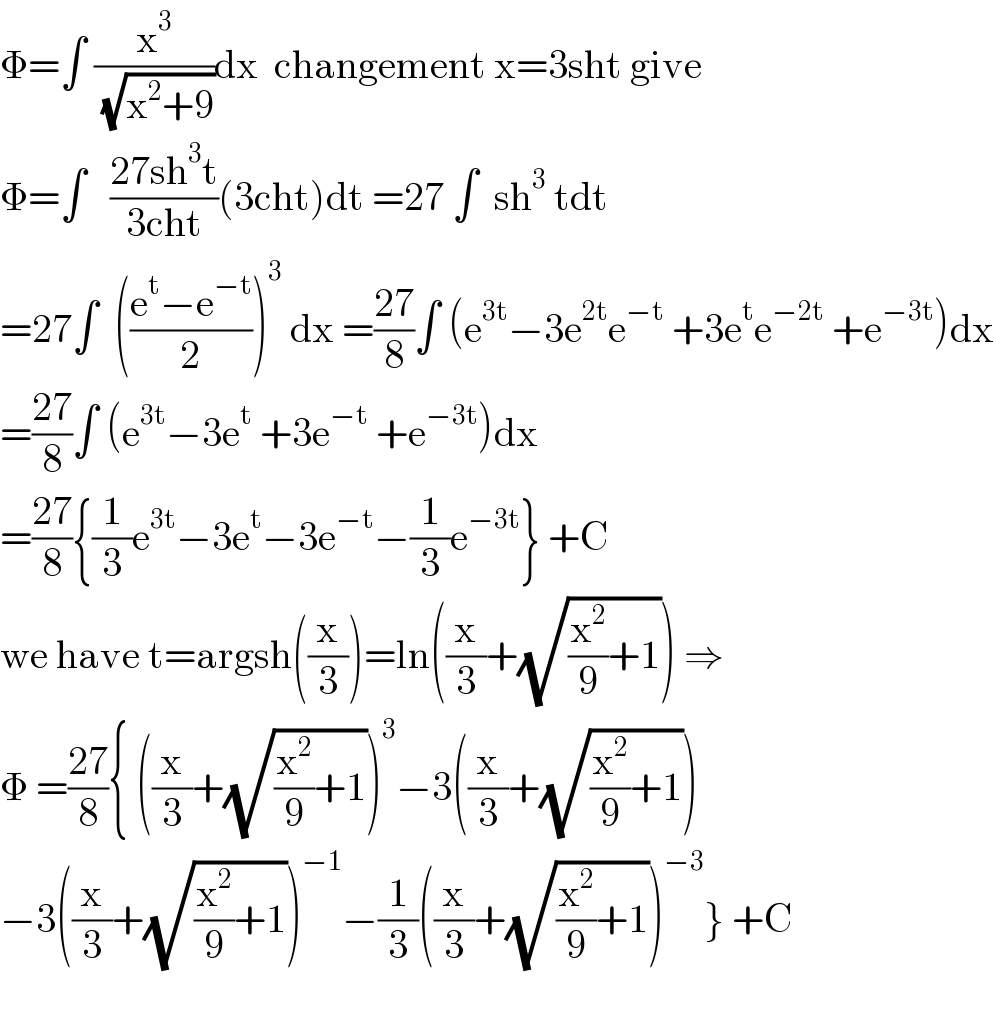
Φ=∫ (x^3 /( (√(x^2 +9))))dx changement x=3sht give Φ=∫ ((27sh^3 t)/(3cht))(3cht)dt =27 ∫ sh^3 tdt =27∫ (((e^t −e^(−t) )/2))^3 dx =((27)/8)∫ (e^(3t) −3e^(2t) e^(−t) +3e^t e^(−2t) +e^(−3t) )dx =((27)/8)∫ (e^(3t) −3e^t +3e^(−t) +e^(−3t) )dx =((27)/8){(1/3)e^(3t) −3e^t −3e^(−t) −(1/3)e^(−3t) } +C we have t=argsh((x/3))=ln((x/3)+(√((x^2 /9)+1))) ⇒ Φ =((27)/8){ ((x/3)+(√((x^2 /9)+1)))^3 −3((x/3)+(√((x^2 /9)+1))) −3((x/3)+(√((x^2 /9)+1)))^(−1) −(1/3)((x/3)+(√((x^2 /9)+1)))^(−3) } +C

$$\Phi=\int\:\frac{\mathrm{x}^{\mathrm{3}} }{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{9}}}\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}=\mathrm{3sht}\:\mathrm{give} \\ $$$$\Phi=\int\:\:\:\frac{\mathrm{27sh}^{\mathrm{3}} \mathrm{t}}{\mathrm{3cht}}\left(\mathrm{3cht}\right)\mathrm{dt}\:=\mathrm{27}\:\int\:\:\mathrm{sh}^{\mathrm{3}} \:\mathrm{tdt} \\ $$$$=\mathrm{27}\int\:\:\left(\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}\right)^{\mathrm{3}} \:\mathrm{dx}\:=\frac{\mathrm{27}}{\mathrm{8}}\int\:\left(\mathrm{e}^{\mathrm{3t}} −\mathrm{3e}^{\mathrm{2t}} \mathrm{e}^{−\mathrm{t}} \:+\mathrm{3e}^{\mathrm{t}} \mathrm{e}^{−\mathrm{2t}} \:+\mathrm{e}^{−\mathrm{3t}} \right)\mathrm{dx} \\ $$$$=\frac{\mathrm{27}}{\mathrm{8}}\int\:\left(\mathrm{e}^{\mathrm{3t}} −\mathrm{3e}^{\mathrm{t}} \:+\mathrm{3e}^{−\mathrm{t}} \:+\mathrm{e}^{−\mathrm{3t}} \right)\mathrm{dx} \\ $$$$=\frac{\mathrm{27}}{\mathrm{8}}\left\{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{\mathrm{3t}} −\mathrm{3e}^{\mathrm{t}} −\mathrm{3e}^{−\mathrm{t}} −\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{−\mathrm{3t}} \right\}\:+\mathrm{C} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{t}=\mathrm{argsh}\left(\frac{\mathrm{x}}{\mathrm{3}}\right)=\mathrm{ln}\left(\frac{\mathrm{x}}{\mathrm{3}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{9}}+\mathrm{1}}\right)\:\Rightarrow \\ $$$$\Phi\:=\frac{\mathrm{27}}{\mathrm{8}}\left\{\:\left(\frac{\mathrm{x}}{\mathrm{3}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{9}}+\mathrm{1}}\right)^{\mathrm{3}} −\mathrm{3}\left(\frac{\mathrm{x}}{\mathrm{3}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{9}}+\mathrm{1}}\right)\right. \\ $$$$\left.−\mathrm{3}\left(\frac{\mathrm{x}}{\mathrm{3}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{9}}+\mathrm{1}}\right)^{−\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{x}}{\mathrm{3}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{9}}+\mathrm{1}}\right)^{−\mathrm{3}} \right\}\:+\mathrm{C} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply