Menu Close

x-3-x-3-1-10-dx-

Tinku Tara 0 Comments
Pin




Question Number 136067 by bramlexs22 last updated on 18/Mar/21
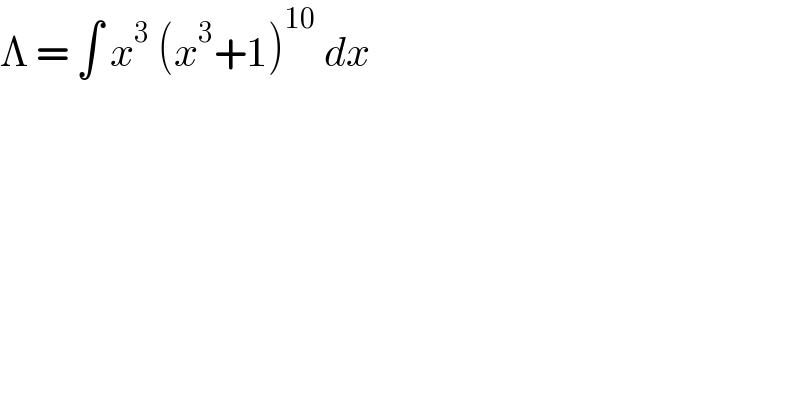
Λ = ∫ x^3 (x^3 +1)^(10) dx
$$\Lambda\:=\:\int\:{x}^{\mathrm{3}} \:\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{10}} \:{dx}\: \\ $$
Answered by Olaf last updated on 18/Mar/21
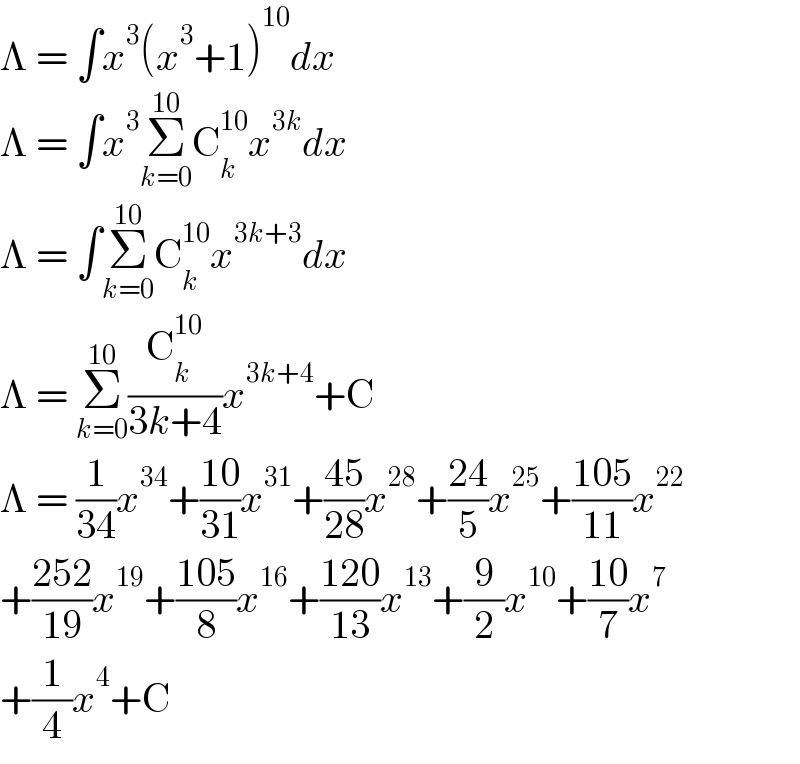
Λ = ∫x^3 (x^3 +1)^(10) dx Λ = ∫x^3 Σ_(k=0) ^(10) C_k ^(10) x^(3k) dx Λ = ∫Σ_(k=0) ^(10) C_k ^(10) x^(3k+3) dx Λ = Σ_(k=0) ^(10) (C_k ^(10) /(3k+4))x^(3k+4) +C Λ = (1/(34))x^(34) +((10)/(31))x^(31) +((45)/(28))x^(28) +((24)/5)x^(25) +((105)/(11))x^(22) +((252)/(19))x^(19) +((105)/8)x^(16) +((120)/(13))x^(13) +(9/2)x^(10) +((10)/7)x^7 +(1/4)x^4 +C
$$\Lambda\:=\:\int{x}^{\mathrm{3}} \left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{10}} {dx} \\ $$$$\Lambda\:=\:\int{x}^{\mathrm{3}} \underset{{k}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}\mathrm{C}_{{k}} ^{\mathrm{10}} {x}^{\mathrm{3}{k}} {dx} \\ $$$$\Lambda\:=\:\int\underset{{k}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}\mathrm{C}_{{k}} ^{\mathrm{10}} {x}^{\mathrm{3}{k}+\mathrm{3}} {dx} \\ $$$$\Lambda\:=\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}\frac{\mathrm{C}_{{k}} ^{\mathrm{10}} }{\mathrm{3}{k}+\mathrm{4}}{x}^{\mathrm{3}{k}+\mathrm{4}} +\mathrm{C} \\ $$$$\Lambda\:=\:\frac{\mathrm{1}}{\mathrm{34}}{x}^{\mathrm{34}} +\frac{\mathrm{10}}{\mathrm{31}}{x}^{\mathrm{31}} +\frac{\mathrm{45}}{\mathrm{28}}{x}^{\mathrm{28}} +\frac{\mathrm{24}}{\mathrm{5}}{x}^{\mathrm{25}} +\frac{\mathrm{105}}{\mathrm{11}}{x}^{\mathrm{22}} \\ $$$$+\frac{\mathrm{252}}{\mathrm{19}}{x}^{\mathrm{19}} +\frac{\mathrm{105}}{\mathrm{8}}{x}^{\mathrm{16}} +\frac{\mathrm{120}}{\mathrm{13}}{x}^{\mathrm{13}} +\frac{\mathrm{9}}{\mathrm{2}}{x}^{\mathrm{10}} +\frac{\mathrm{10}}{\mathrm{7}}{x}^{\mathrm{7}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{4}} +\mathrm{C} \\ $$
Commented by bramlexs22 last updated on 19/Mar/21
yes....thanks
$${yes}….{thanks} \\ $$
Answered by Ñï= last updated on 18/Mar/21
Λ=∫x^3 (x^3 +1)^(10) dx =(1/(33))∫xd[(x^3 +1)^(11) ] =(1/(33)){(x^3 +1)^(11) x−∫(x^3 +1)^(11) dx} =(1/(33))(x^3 +1)^(11) x−(1/(33))Σ_(n=0) ^(11) (((11)),(n) )∫x^3 dx =(1/(33))(x^3 +1)^(11) x−(1/(132))Σ_(n=0) ^(11) (((11)),(n) )x^4 +C
$$\Lambda=\int{x}^{\mathrm{3}} \left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{10}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{33}}\int{xd}\left[\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{11}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{33}}\left\{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{11}} {x}−\int\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{11}} {dx}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{33}}\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{11}} {x}−\frac{\mathrm{1}}{\mathrm{33}}\underset{{n}=\mathrm{0}} {\overset{\mathrm{11}} {\sum}}\begin{pmatrix}{\mathrm{11}}\\{{n}}\end{pmatrix}\int{x}^{\mathrm{3}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{33}}\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{11}} {x}−\frac{\mathrm{1}}{\mathrm{132}}\underset{{n}=\mathrm{0}} {\overset{\mathrm{11}} {\sum}}\begin{pmatrix}{\mathrm{11}}\\{{n}}\end{pmatrix}{x}^{\mathrm{4}} +{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *