Menu Close

x-3-x-4-dx-

Tinku Tara 0 Comments
Pin




Question Number 77290 by TawaTawa last updated on 05/Jan/20
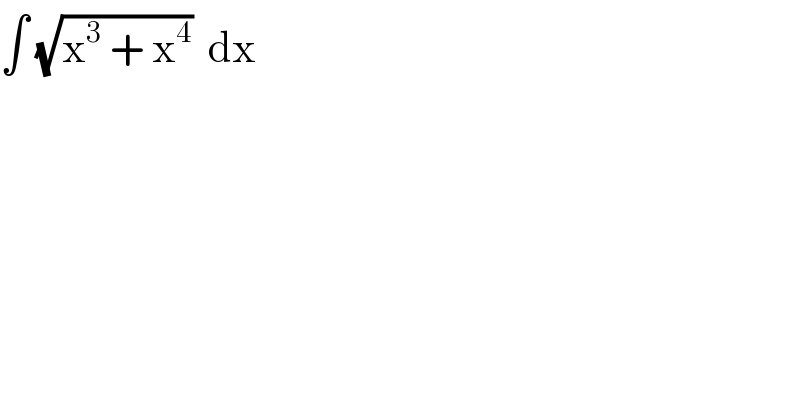
∫ (√(x^3 + x^4 )) dx
$$\int\:\sqrt{\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{x}^{\mathrm{4}} }\:\:\mathrm{dx} \\ $$
Commented by mathmax by abdo last updated on 05/Jan/20
let I =∫(√(x^3 +x^4 ))dx ⇒ I =∫(√(x^3 (1+x)))dx =∫ x^(3/2) (√(1+x))dx changement (√(1+x))=t hive 1+x=t^2 ⇒ I =∫(t^2 −1)^(3/2) t(2t)dt =2 ∫t^2 (t^2 −1)^(3/2) dt =_(t=ch(u)) 2 ∫ch^2 u(sh^2 u)^(3/2) sh(u)du =2 ∫ ch^2 u sh^4 u du =2∫(((sh(2u))/2))^2 sh^2 u du =(1/2)∫ sh^2 (2u)sh^2 (u)du =(1/2)∫((ch(4u)−1)/2)×((ch(2u)−1)/2)du =(1/8)∫(ch(4u)−1)(ch(2u)−1)du ⇒ 8I =∫(ch(4u)ch(2u)−ch(4u)−ch(2u)+1)du =∫ (((e^(4u) +e^(−4u) )(e^(2u) +e^(−2u) ))/4)du−(1/4)sh(4u)−(1/2)sh(2u) +u +c =(1/4)∫(e^(6u) +e^(2u) +e^(−2u) +e^(−6u) )−(1/8)(e^(4u) −e^(−4u) )−(1/2)(e^(2u) −e^(−2u) ) +u +c =(1/(24))e^(6u) −(1/(24))e^(−6u) +(1/8)e^(2u) −(1/8)e^(−2u) −(1/8)e^(4u) +(1/8)e^(−4u) −(1/2)e^(2u) +(1/2)e^(−2u) +u +c =(1/(24))e^(6ln(t+(√(t^2 −1)))) −(1/(24)) e^(−6ln(t+(√(t^2 −1)))) +(1/8)e^(2ln(g+(√(t^2 −1)))) −(1/8)e^(−2ln(t+(√(t^2 −1)))) −(1/8)e^(4ln(t+(√(t^2 −1)))) +(1/8)e^(−4ln(t+(√(t^2 −1)))) −(1/2)e^(2ln(t+(√(t^2 −1)))) +(1/2)e^(−2ln(t+(√(t^2 −1)))) +ln(t+(√(t^2 −1))) +c =(1/(24))(t+(√(t^2 −1)))^6 −(1/(24(t+(√(t^2 −1)))^6 )) +(1/8)(t+(√(t^2 −1)))^2 −(1/(8(t+(√(t^2 −1)))^2 )) −(1/8)(t+(√(t^2 −1)))^4 +(1/(8(t+(√(t^2 −1)))^4 ))−(1/2)(t+(√(t^2 −1)))^2 +(1/(2(t+(√(t^2 −1)))^2 )) +ln(t+(√(t^2 −1))) +C =(1/(24))((√(1+x))+(√x))^6 −(1/(24((√(1+x))+(√x))^6 )) +(1/8)((√(1+x))+(√x))^2 −(1/(8((√(1+x))+(√x))^2 ))−(1/8)((√(1+x))+(√x))^4 +(1/(8((√(1+x))+(√x))^4 ))−(1/2)((√(1+x))+(√x))^2 +(1/(2((√(1+x))+(√x))^2 )) +ln((√(1+x))+(√x)) +C .
$${let}\:{I}\:=\int\sqrt{{x}^{\mathrm{3}} \:+{x}^{\mathrm{4}} }{dx}\:\Rightarrow\:{I}\:=\int\sqrt{{x}^{\mathrm{3}} \left(\mathrm{1}+{x}\right)}{dx}\:=\int\:{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \sqrt{\mathrm{1}+{x}}{dx} \\ $$$${changement}\:\sqrt{\mathrm{1}+{x}}={t}\:{hive}\:\mathrm{1}+{x}={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${I}\:=\int\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {t}\left(\mathrm{2}{t}\right){dt}\:=\mathrm{2}\:\int{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {dt}\:=_{{t}={ch}\left({u}\right)} \mathrm{2}\:\int{ch}^{\mathrm{2}} {u}\left({sh}^{\mathrm{2}} {u}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {sh}\left({u}\right){du} \\ $$$$=\mathrm{2}\:\int\:{ch}^{\mathrm{2}} {u}\:{sh}^{\mathrm{4}} {u}\:{du}\:=\mathrm{2}\int\left(\frac{{sh}\left(\mathrm{2}{u}\right)}{\mathrm{2}}\right)^{\mathrm{2}} {sh}^{\mathrm{2}} {u}\:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:{sh}^{\mathrm{2}} \left(\mathrm{2}{u}\right){sh}^{\mathrm{2}} \left({u}\right){du}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{ch}\left(\mathrm{4}{u}\right)−\mathrm{1}}{\mathrm{2}}×\frac{{ch}\left(\mathrm{2}{u}\right)−\mathrm{1}}{\mathrm{2}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\left({ch}\left(\mathrm{4}{u}\right)−\mathrm{1}\right)\left({ch}\left(\mathrm{2}{u}\right)−\mathrm{1}\right){du}\:\Rightarrow \\ $$$$\mathrm{8}{I}\:=\int\left({ch}\left(\mathrm{4}{u}\right){ch}\left(\mathrm{2}{u}\right)−{ch}\left(\mathrm{4}{u}\right)−{ch}\left(\mathrm{2}{u}\right)+\mathrm{1}\right){du} \\ $$$$=\int\:\:\frac{\left({e}^{\mathrm{4}{u}} +{e}^{−\mathrm{4}{u}} \right)\left({e}^{\mathrm{2}{u}} +{e}^{−\mathrm{2}{u}} \right)}{\mathrm{4}}{du}−\frac{\mathrm{1}}{\mathrm{4}}{sh}\left(\mathrm{4}{u}\right)−\frac{\mathrm{1}}{\mathrm{2}}{sh}\left(\mathrm{2}{u}\right)\:+{u}\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\left({e}^{\mathrm{6}{u}} +{e}^{\mathrm{2}{u}} +{e}^{−\mathrm{2}{u}} \:+{e}^{−\mathrm{6}{u}} \right)−\frac{\mathrm{1}}{\mathrm{8}}\left({e}^{\mathrm{4}{u}} −{e}^{−\mathrm{4}{u}} \right)−\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{\mathrm{2}{u}} −{e}^{−\mathrm{2}{u}} \right)\:+{u}\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}{e}^{\mathrm{6}{u}} \:−\frac{\mathrm{1}}{\mathrm{24}}{e}^{−\mathrm{6}{u}} \:+\frac{\mathrm{1}}{\mathrm{8}}{e}^{\mathrm{2}{u}} −\frac{\mathrm{1}}{\mathrm{8}}{e}^{−\mathrm{2}{u}} −\frac{\mathrm{1}}{\mathrm{8}}{e}^{\mathrm{4}{u}} +\frac{\mathrm{1}}{\mathrm{8}}{e}^{−\mathrm{4}{u}} −\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{2}{u}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\mathrm{2}{u}} \:\:+{u}\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}{e}^{\mathrm{6}{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)} −\frac{\mathrm{1}}{\mathrm{24}}\:{e}^{−\mathrm{6}{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)} \:+\frac{\mathrm{1}}{\mathrm{8}}{e}^{\mathrm{2}{ln}\left({g}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)} −\frac{\mathrm{1}}{\mathrm{8}}{e}^{−\mathrm{2}{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)} \\ $$$$−\frac{\mathrm{1}}{\mathrm{8}}{e}^{\mathrm{4}{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)} \:+\frac{\mathrm{1}}{\mathrm{8}}{e}^{−\mathrm{4}{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)} −\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{2}{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)} \:+\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\mathrm{2}{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)} \\ $$$$+{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{6}} \:−\frac{\mathrm{1}}{\mathrm{24}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{6}} }\:+\frac{\mathrm{1}}{\mathrm{8}}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} \:−\frac{\mathrm{1}}{\mathrm{8}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$−\frac{\mathrm{1}}{\mathrm{8}}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{4}} \:+\frac{\mathrm{1}}{\mathrm{8}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{2}}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$+{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)\:+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}\left(\sqrt{\mathrm{1}+{x}}+\sqrt{{x}}\right)^{\mathrm{6}} −\frac{\mathrm{1}}{\mathrm{24}\left(\sqrt{\mathrm{1}+{x}}+\sqrt{{x}}\right)^{\mathrm{6}} }\:+\frac{\mathrm{1}}{\mathrm{8}}\left(\sqrt{\mathrm{1}+{x}}+\sqrt{{x}}\right)^{\mathrm{2}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{8}\left(\sqrt{\mathrm{1}+{x}}+\sqrt{{x}}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{8}}\left(\sqrt{\mathrm{1}+{x}}+\sqrt{{x}}\right)^{\mathrm{4}} \:+\frac{\mathrm{1}}{\mathrm{8}\left(\sqrt{\mathrm{1}+{x}}+\sqrt{{x}}\right)^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{1}+{x}}+\sqrt{{x}}\right)^{\mathrm{2}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}\left(\sqrt{\mathrm{1}+{x}}+\sqrt{{x}}\right)^{\mathrm{2}} }\:+{ln}\left(\sqrt{\mathrm{1}+{x}}+\sqrt{{x}}\right)\:+{C}\:. \\ $$$$ \\ $$
Commented by TawaTawa last updated on 05/Jan/20
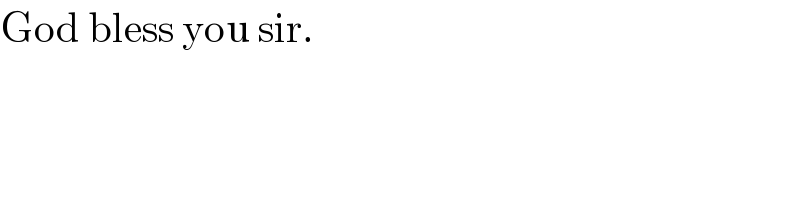
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mathmax by abdo last updated on 05/Jan/20
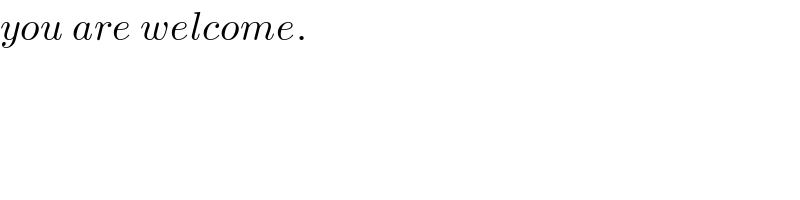
you are welcome.
$${you}\:{are}\:{welcome}. \\ $$
Answered by petrochengula last updated on 05/Jan/20
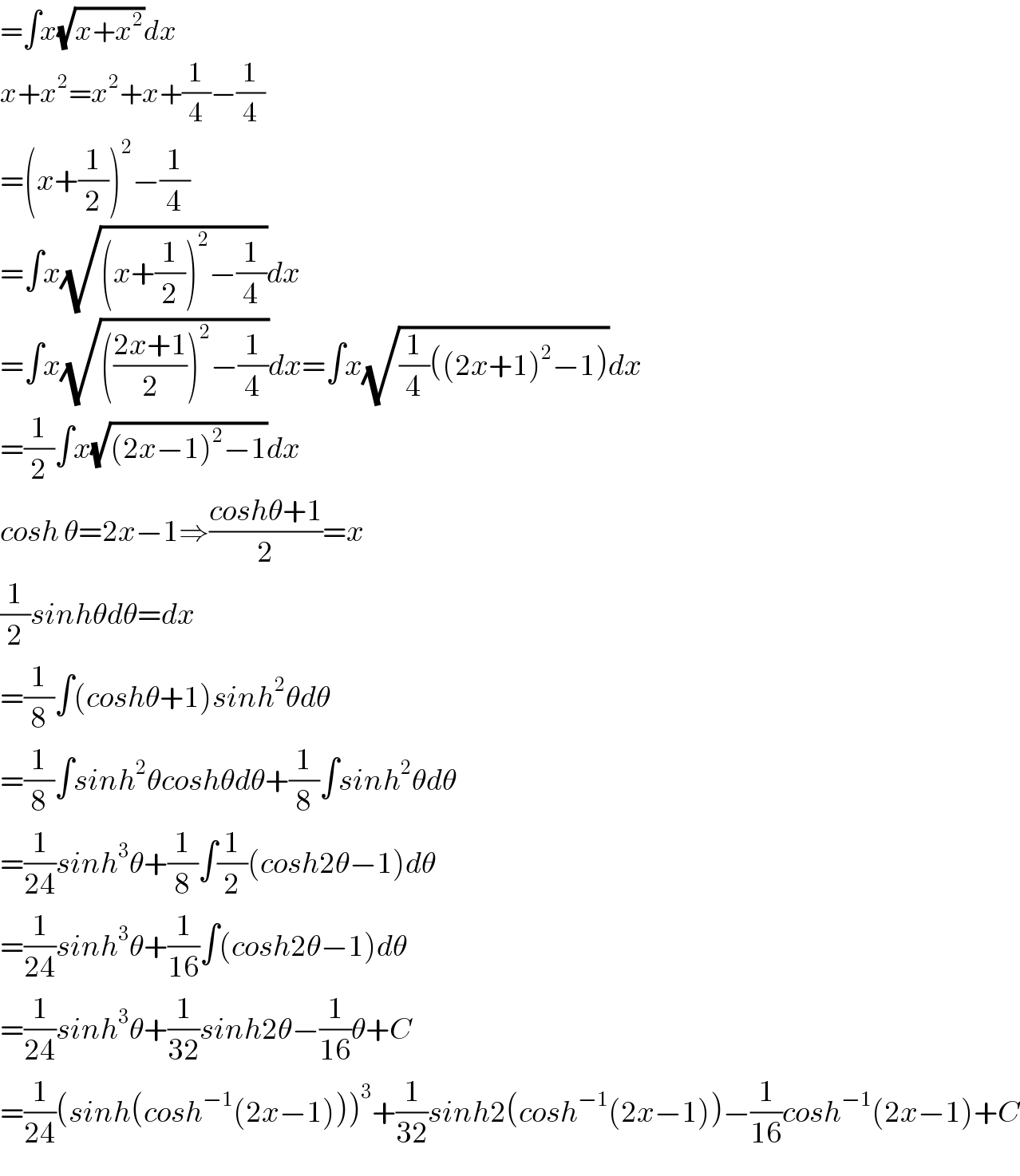
=∫x(√(x+x^2 ))dx x+x^2 =x^2 +x+(1/4)−(1/4) =(x+(1/2))^2 −(1/4) =∫x(√((x+(1/2))^2 −(1/4)))dx =∫x(√((((2x+1)/2))^2 −(1/4)))dx=∫x(√((1/4)((2x+1)^2 −1)))dx =(1/2)∫x(√((2x−1)^2 −1))dx cosh θ=2x−1⇒((coshθ+1)/2)=x (1/2)sinhθdθ=dx =(1/8)∫(coshθ+1)sinh^2 θdθ =(1/8)∫sinh^2 θcoshθdθ+(1/8)∫sinh^2 θdθ =(1/(24))sinh^3 θ+(1/8)∫(1/2)(cosh2θ−1)dθ =(1/(24))sinh^3 θ+(1/(16))∫(cosh2θ−1)dθ =(1/(24))sinh^3 θ+(1/(32))sinh2θ−(1/(16))θ+C =(1/(24))(sinh(cosh^(−1) (2x−1)))^3 +(1/(32))sinh2(cosh^(−1) (2x−1))−(1/(16))cosh^(−1) (2x−1)+C
$$=\int{x}\sqrt{{x}+{x}^{\mathrm{2}} }{dx} \\ $$$${x}+{x}^{\mathrm{2}} ={x}^{\mathrm{2}} +{x}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$=\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$=\int{x}\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}{dx} \\ $$$$=\int{x}\sqrt{\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}{dx}=\int{x}\sqrt{\frac{\mathrm{1}}{\mathrm{4}}\left(\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{x}\sqrt{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}{dx} \\ $$$${cosh}\:\theta=\mathrm{2}{x}−\mathrm{1}\Rightarrow\frac{{cosh}\theta+\mathrm{1}}{\mathrm{2}}={x} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{sinh}\theta{d}\theta={dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\left({cosh}\theta+\mathrm{1}\right){sinh}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int{sinh}^{\mathrm{2}} \theta{cosh}\theta{d}\theta+\frac{\mathrm{1}}{\mathrm{8}}\int{sinh}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}{sinh}^{\mathrm{3}} \theta+\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\mathrm{1}}{\mathrm{2}}\left({cosh}\mathrm{2}\theta−\mathrm{1}\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}{sinh}^{\mathrm{3}} \theta+\frac{\mathrm{1}}{\mathrm{16}}\int\left({cosh}\mathrm{2}\theta−\mathrm{1}\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}{sinh}^{\mathrm{3}} \theta+\frac{\mathrm{1}}{\mathrm{32}}{sinh}\mathrm{2}\theta−\frac{\mathrm{1}}{\mathrm{16}}\theta+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}\left({sinh}\left({cosh}^{−\mathrm{1}} \left(\mathrm{2}{x}−\mathrm{1}\right)\right)\right)^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{32}}{sinh}\mathrm{2}\left({cosh}^{−\mathrm{1}} \left(\mathrm{2}{x}−\mathrm{1}\right)\right)−\frac{\mathrm{1}}{\mathrm{16}}{cosh}^{−\mathrm{1}} \left(\mathrm{2}{x}−\mathrm{1}\right)+{C} \\ $$
Commented by petrochengula last updated on 05/Jan/20
please check
$${please}\:{check} \\ $$
Commented by TawaTawa last updated on 05/Jan/20
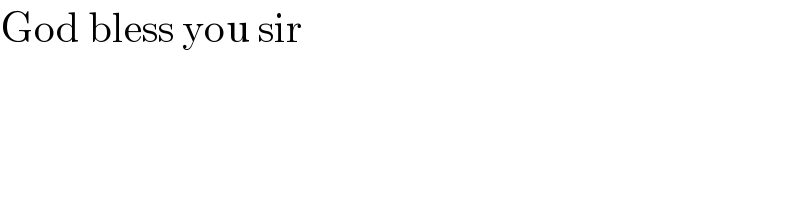
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by petrochengula last updated on 05/Jan/20
thanks
$${thanks} \\ $$
Answered by MJS last updated on 05/Jan/20
∫(√(x^4 +x^3 ))dx=∫x(√(x(x+1)))dx= [t=(√(x(x+1))) → dx=((2(√(x(x+1))))/(2x+1))dt] =∫t^2 dt−∫(t^2 /( (√(4t^2 +1))))dt= ∫(t^2 /( (√(4t^2 +1))))dt= [u=(√(4t^2 +1)) → dt=((√(4t^2 +1))/(4t))du] =(1/8)∫(√(u^2 −1))du and this should be easy =(1/3)t^3 −(1/8)t(√(4t^2 +1))+(1/(16))ln (2t+(√(4t^2 +1))) = =(1/(24))(8x^2 +2x−3)(√(x(x+1)))+(1/(16))ln (2x+1+2(√(x(x+1)))) +C
$$\int\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{3}} }{dx}=\int{x}\sqrt{{x}\left({x}+\mathrm{1}\right)}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}\left({x}+\mathrm{1}\right)}\:\rightarrow\:{dx}=\frac{\mathrm{2}\sqrt{{x}\left({x}+\mathrm{1}\right)}}{\mathrm{2}{x}+\mathrm{1}}{dt}\right] \\ $$$$=\int{t}^{\mathrm{2}} {dt}−\int\frac{{t}^{\mathrm{2}} }{\:\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}}}{dt}= \\ $$$$ \\ $$$$\:\:\:\:\:\int\frac{{t}^{\mathrm{2}} }{\:\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}}}{dt}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{u}=\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dt}=\frac{\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{4}{t}}{du}\right] \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{8}}\int\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}{du}\:\mathrm{and}\:\mathrm{this}\:\mathrm{should}\:\mathrm{be}\:\mathrm{easy} \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{t}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{8}}{t}\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{16}}\mathrm{ln}\:\left(\mathrm{2}{t}+\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}}\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}\left(\mathrm{8}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}\right)\sqrt{{x}\left({x}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{16}}\mathrm{ln}\:\left(\mathrm{2}{x}+\mathrm{1}+\mathrm{2}\sqrt{{x}\left({x}+\mathrm{1}\right)}\right)\:+{C} \\ $$
Commented by TawaTawa last updated on 05/Jan/20
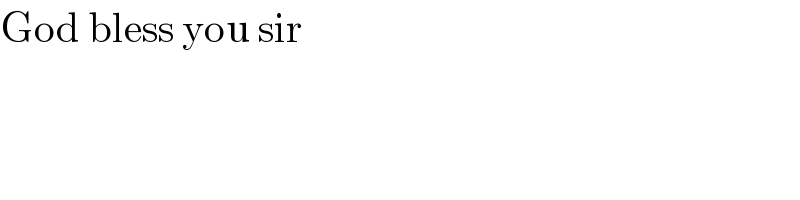
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *