Question Number 133291 by liberty last updated on 21/Feb/21
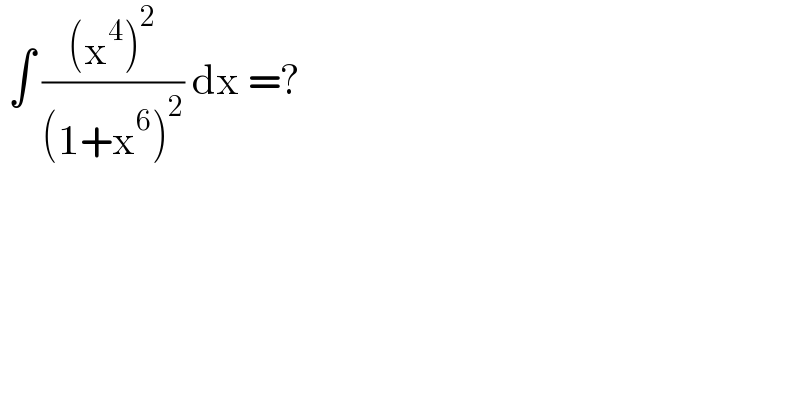
$$\:\int\:\frac{\left(\mathrm{x}^{\mathrm{4}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{6}} \right)^{\mathrm{2}} }\:\mathrm{dx}\:=? \\ $$
Answered by EDWIN88 last updated on 21/Feb/21

$$\mathrm{integration}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{x}^{\mathrm{3}} \:.\:\mathrm{x}^{\mathrm{5}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{6}} \right)^{\mathrm{2}} }\mathrm{dx}\:\rightarrow\begin{cases}{\mathrm{u}=\mathrm{x}^{\mathrm{3}} \rightarrow\mathrm{du}=\mathrm{3x}^{\mathrm{2}} \:\mathrm{dx}}\\{\mathrm{v}=\int\:\frac{\mathrm{x}^{\mathrm{5}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{6}} \right)^{\mathrm{2}} }\mathrm{dx}=−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{6}} }}\end{cases} \\ $$$$\mathrm{I}=\:−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{1}+\mathrm{x}^{\mathrm{6}} }\:+\:\int\:\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{6}} }\:\mathrm{dx}\: \\ $$$$\mathrm{let}\:\mathrm{x}^{\mathrm{3}} \:=\:\mathrm{tan}\:\varphi\:\Rightarrow\mathrm{3x}^{\mathrm{2}} \:\mathrm{dx}\:=\:\mathrm{sec}\:^{\mathrm{2}} \varphi\:\mathrm{d}\varphi \\ $$$$\mathrm{I}=−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{1}+\mathrm{x}^{\mathrm{6}} }\:+\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \varphi\:\mathrm{d}\varphi}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \varphi} \\ $$$$\mathrm{I}=−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{1}+\mathrm{x}^{\mathrm{6}} }\:+\:\mathrm{arctan}\:\left(\mathrm{x}^{\mathrm{3}} \right)\:+\:\mathrm{c}\: \\ $$
