Question Number 65853 by ajfour last updated on 05/Aug/19
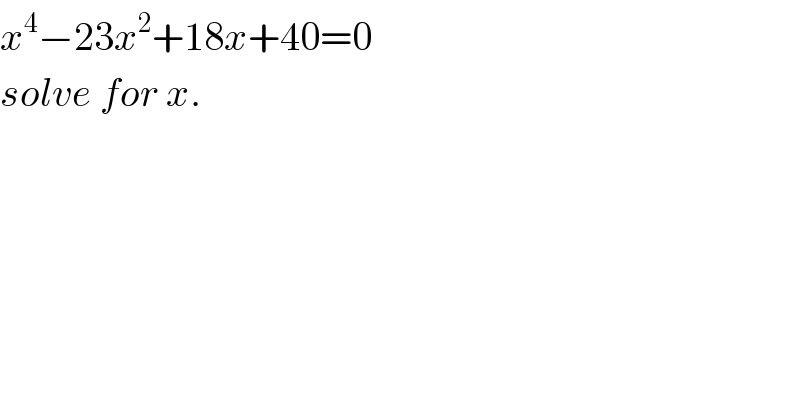
$${x}^{\mathrm{4}} −\mathrm{23}{x}^{\mathrm{2}} +\mathrm{18}{x}+\mathrm{40}=\mathrm{0} \\ $$$${solve}\:{for}\:{x}. \\ $$
Answered by ajfour last updated on 05/Aug/19
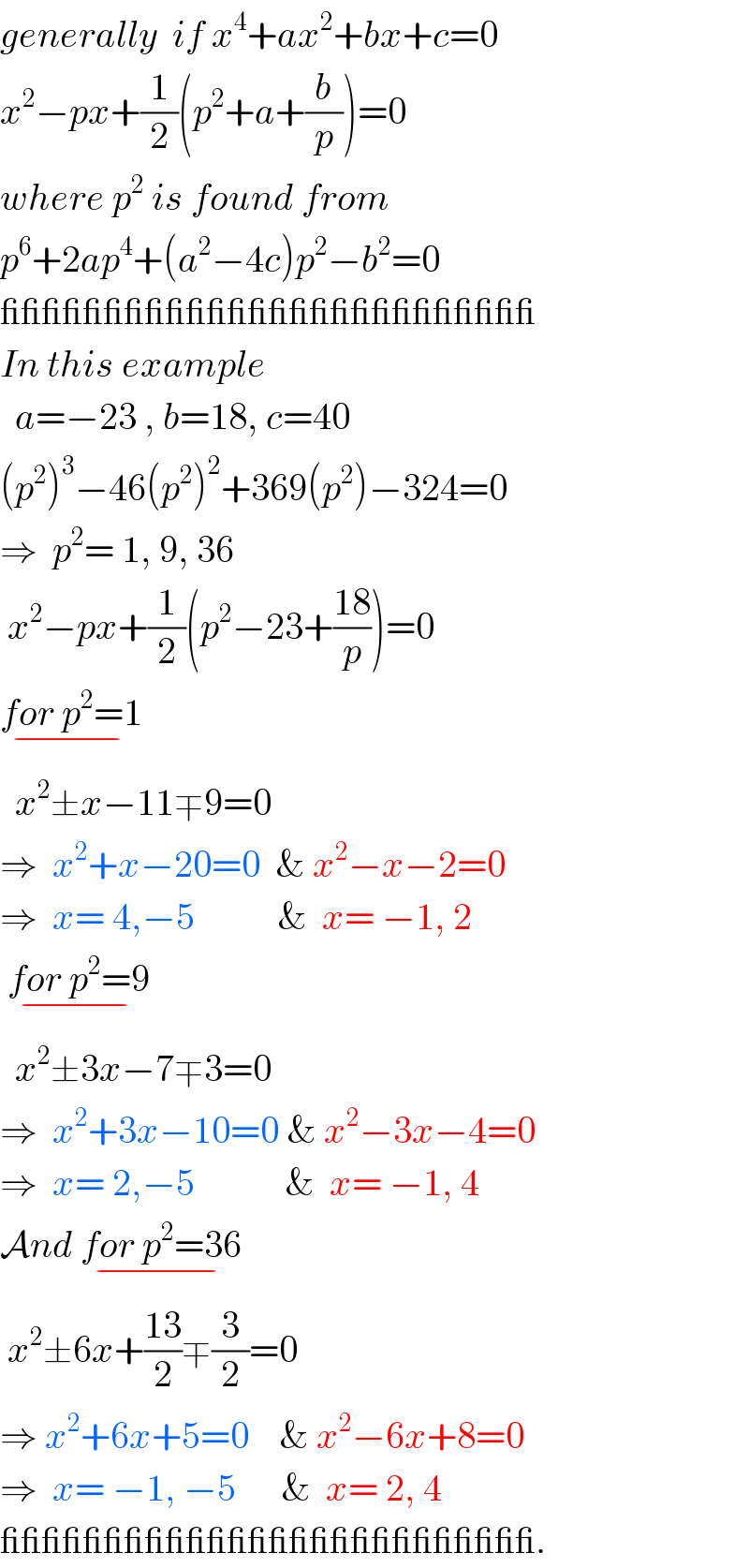
$${generally}\:\:{if}\:{x}^{\mathrm{4}} +{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{px}+\frac{\mathrm{1}}{\mathrm{2}}\left({p}^{\mathrm{2}} +{a}+\frac{{b}}{{p}}\right)=\mathrm{0} \\ $$$${where}\:{p}^{\mathrm{2}} \:{is}\:{found}\:{from} \\ $$$${p}^{\mathrm{6}} +\mathrm{2}{ap}^{\mathrm{4}} +\left({a}^{\mathrm{2}} −\mathrm{4}{c}\right){p}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${In}\:{this}\:{example} \\ $$$$\:\:{a}=−\mathrm{23}\:,\:{b}=\mathrm{18},\:{c}=\mathrm{40} \\ $$$$\left({p}^{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{46}\left({p}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{369}\left({p}^{\mathrm{2}} \right)−\mathrm{324}=\mathrm{0} \\ $$$$\Rightarrow\:\:{p}^{\mathrm{2}} =\:\mathrm{1},\:\mathrm{9},\:\mathrm{36} \\ $$$$\:{x}^{\mathrm{2}} −{px}+\frac{\mathrm{1}}{\mathrm{2}}\left({p}^{\mathrm{2}} −\mathrm{23}+\frac{\mathrm{18}}{{p}}\right)=\mathrm{0} \\ $$$$\underset{−} {{for}\:{p}^{\mathrm{2}} =\mathrm{1}} \\ $$$$\:\:{x}^{\mathrm{2}} \pm{x}−\mathrm{11}\mp\mathrm{9}=\mathrm{0} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} +{x}−\mathrm{20}=\mathrm{0}\:\:\&\:{x}^{\mathrm{2}} −{x}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\:\:{x}=\:\mathrm{4},−\mathrm{5}\:\:\:\:\:\:\:\:\:\:\:\&\:\:{x}=\:−\mathrm{1},\:\mathrm{2}\:\:\: \\ $$$$\:\underset{−} {{for}\:{p}^{\mathrm{2}} =\mathrm{9}} \\ $$$$\:\:{x}^{\mathrm{2}} \pm\mathrm{3}{x}−\mathrm{7}\mp\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{10}=\mathrm{0}\:\&\:{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\:\:{x}=\:\mathrm{2},−\mathrm{5}\:\:\:\:\:\:\:\:\:\:\:\:\&\:\:{x}=\:−\mathrm{1},\:\mathrm{4} \\ $$$$\mathcal{A}{nd}\:\underset{−} {{for}\:{p}^{\mathrm{2}} =\mathrm{36}} \\ $$$$\:{x}^{\mathrm{2}} \pm\mathrm{6}{x}+\frac{\mathrm{13}}{\mathrm{2}}\mp\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{5}=\mathrm{0}\:\:\:\:\&\:{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{8}=\mathrm{0} \\ $$$$\Rightarrow\:\:{x}=\:−\mathrm{1},\:−\mathrm{5}\:\:\:\:\:\:\&\:\:{x}=\:\mathrm{2},\:\mathrm{4}\: \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_. \\ $$
Commented by TawaTawa last updated on 05/Aug/19
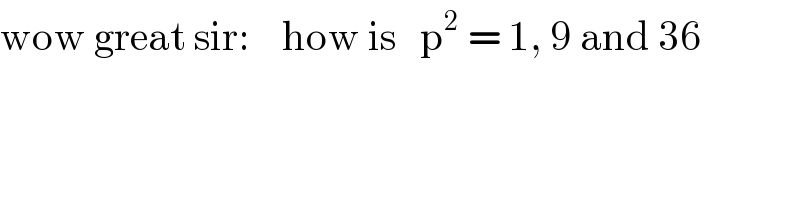
$$\mathrm{wow}\:\mathrm{great}\:\mathrm{sir}:\:\:\:\:\mathrm{how}\:\mathrm{is}\:\:\:\mathrm{p}^{\mathrm{2}} \:=\:\mathrm{1},\:\mathrm{9}\:\mathrm{and}\:\mathrm{36} \\ $$
