x-4-5x-2-20x-104-0-solve-for-x-

Question Number 65859 by ajfour last updated on 05/Aug/19

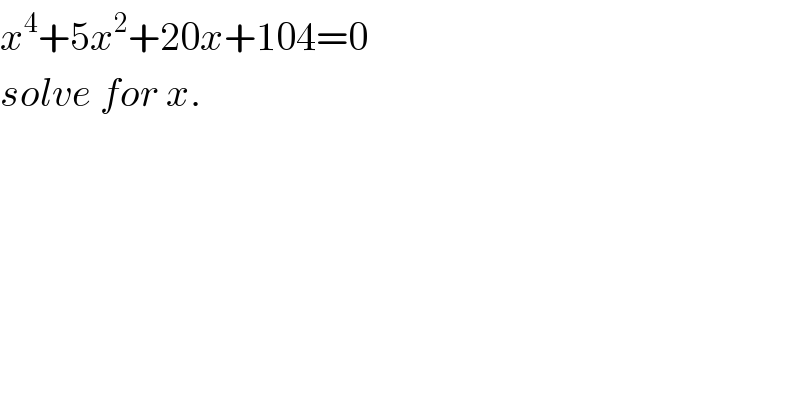
$${x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{20}{x}+\mathrm{104}=\mathrm{0} \\ $$$${solve}\:{for}\:{x}. \\ $$

Answered by ajfour last updated on 05/Aug/19

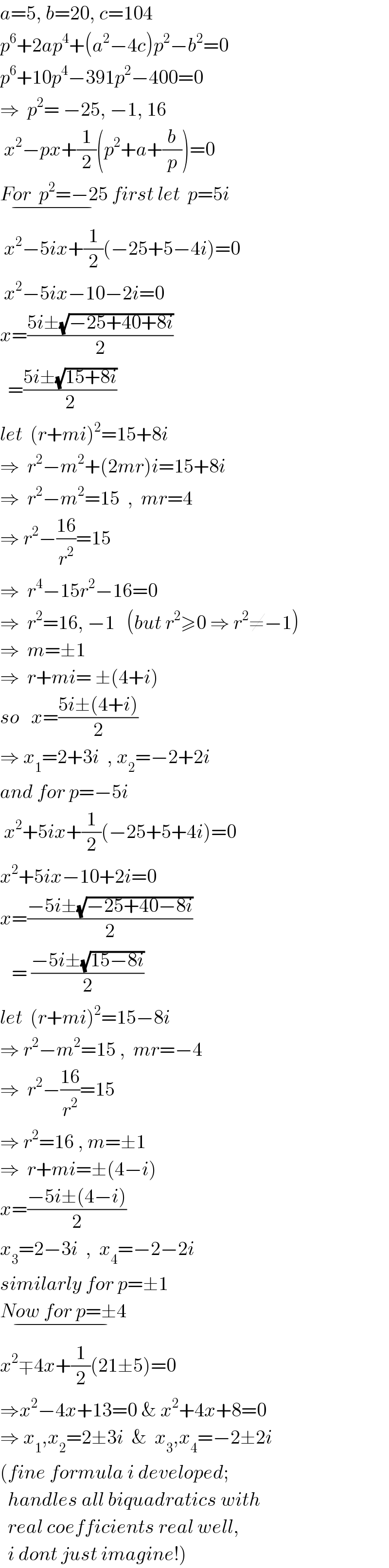
a=5, b=20, c=104 p^6 +2ap^4 +(a^2 −4c)p^2 −b^2 =0 p^6 +10p^4 −391p^2 −400=0 ⇒ p^2 = −25, −1, 16 x^2 −px+(1/2)(p^2 +a+(b/p))=0 For p^2 =−25_(−) first let p=5i x^2 −5ix+(1/2)(−25+5−4i)=0 x^2 −5ix−10−2i=0 x=((5i±(√(−25+40+8i)))/2) =((5i±(√(15+8i)))/2) let (r+mi)^2 =15+8i ⇒ r^2 −m^2 +(2mr)i=15+8i ⇒ r^2 −m^2 =15 , mr=4 ⇒ r^2 −((16)/r^2 )=15 ⇒ r^4 −15r^2 −16=0 ⇒ r^2 =16, −1 (but r^2 ≥0 ⇒ r^2 ≠−1) ⇒ m=±1 ⇒ r+mi= ±(4+i) so x=((5i±(4+i))/2) ⇒ x_1 =2+3i , x_2 =−2+2i and for p=−5i x^2 +5ix+(1/2)(−25+5+4i)=0 x^2 +5ix−10+2i=0 x=((−5i±(√(−25+40−8i)))/2) = ((−5i±(√(15−8i)))/2) let (r+mi)^2 =15−8i ⇒ r^2 −m^2 =15 , mr=−4 ⇒ r^2 −((16)/r^2 )=15 ⇒ r^2 =16 , m=±1 ⇒ r+mi=±(4−i) x=((−5i±(4−i))/2) x_3 =2−3i , x_4 =−2−2i similarly for p=±1 Now for p=±4_(−) x^2 ∓4x+(1/2)(21±5)=0 ⇒x^2 −4x+13=0 & x^2 +4x+8=0 ⇒ x_1 ,x_2 =2±3i & x_3 ,x_4 =−2±2i (fine formula i developed; handles all biquadratics with real coefficients real well, i dont just imagine!)

$${a}=\mathrm{5},\:{b}=\mathrm{20},\:{c}=\mathrm{104} \\ $$$${p}^{\mathrm{6}} +\mathrm{2}{ap}^{\mathrm{4}} +\left({a}^{\mathrm{2}} −\mathrm{4}{c}\right){p}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0} \\ $$$${p}^{\mathrm{6}} +\mathrm{10}{p}^{\mathrm{4}} −\mathrm{391}{p}^{\mathrm{2}} −\mathrm{400}=\mathrm{0} \\ $$$$\Rightarrow\:\:{p}^{\mathrm{2}} =\:−\mathrm{25},\:−\mathrm{1},\:\mathrm{16} \\ $$$$\:{x}^{\mathrm{2}} −{px}+\frac{\mathrm{1}}{\mathrm{2}}\left({p}^{\mathrm{2}} +{a}+\frac{{b}}{{p}}\right)=\mathrm{0} \\ $$$$\underset{−} {{For}\:\:{p}^{\mathrm{2}} =−\mathrm{25}}\:{first}\:{let}\:\:{p}=\mathrm{5}{i} \\ $$$$\:{x}^{\mathrm{2}} −\mathrm{5}{ix}+\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{25}+\mathrm{5}−\mathrm{4}{i}\right)=\mathrm{0} \\ $$$$\:{x}^{\mathrm{2}} −\mathrm{5}{ix}−\mathrm{10}−\mathrm{2}{i}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{5}{i}\pm\sqrt{−\mathrm{25}+\mathrm{40}+\mathrm{8}{i}}}{\mathrm{2}} \\ $$$$\:\:=\frac{\mathrm{5}{i}\pm\sqrt{\mathrm{15}+\mathrm{8}{i}}}{\mathrm{2}} \\ $$$${let}\:\:\left({r}+{mi}\right)^{\mathrm{2}} =\mathrm{15}+\mathrm{8}{i} \\ $$$$\Rightarrow\:\:{r}^{\mathrm{2}} −{m}^{\mathrm{2}} +\left(\mathrm{2}{mr}\right){i}=\mathrm{15}+\mathrm{8}{i} \\ $$$$\Rightarrow\:\:{r}^{\mathrm{2}} −{m}^{\mathrm{2}} =\mathrm{15}\:\:,\:\:{mr}=\mathrm{4} \\ $$$$\Rightarrow\:{r}^{\mathrm{2}} −\frac{\mathrm{16}}{{r}^{\mathrm{2}} }=\mathrm{15} \\ $$$$\Rightarrow\:\:{r}^{\mathrm{4}} −\mathrm{15}{r}^{\mathrm{2}} −\mathrm{16}=\mathrm{0} \\ $$$$\Rightarrow\:\:{r}^{\mathrm{2}} =\mathrm{16},\:−\mathrm{1}\:\:\:\left({but}\:{r}^{\mathrm{2}} \geqslant\mathrm{0}\:\Rightarrow\:{r}^{\mathrm{2}} \neq−\mathrm{1}\right) \\ $$$$\Rightarrow\:\:{m}=\pm\mathrm{1} \\ $$$$\Rightarrow\:\:{r}+{mi}=\:\pm\left(\mathrm{4}+{i}\right) \\ $$$${so}\:\:\:{x}=\frac{\mathrm{5}{i}\pm\left(\mathrm{4}+{i}\right)}{\mathrm{2}}\: \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} =\mathrm{2}+\mathrm{3}{i}\:\:,\:{x}_{\mathrm{2}} =−\mathrm{2}+\mathrm{2}{i} \\ $$$${and}\:{for}\:{p}=−\mathrm{5}{i} \\ $$$$\:{x}^{\mathrm{2}} +\mathrm{5}{ix}+\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{25}+\mathrm{5}+\mathrm{4}{i}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\mathrm{5}{ix}−\mathrm{10}+\mathrm{2}{i}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{5}{i}\pm\sqrt{−\mathrm{25}+\mathrm{40}−\mathrm{8}{i}}}{\mathrm{2}} \\ $$$$\:\:\:=\:\frac{−\mathrm{5}{i}\pm\sqrt{\mathrm{15}−\mathrm{8}{i}}}{\mathrm{2}} \\ $$$${let}\:\:\left({r}+{mi}\right)^{\mathrm{2}} =\mathrm{15}−\mathrm{8}{i} \\ $$$$\Rightarrow\:{r}^{\mathrm{2}} −{m}^{\mathrm{2}} =\mathrm{15}\:,\:\:{mr}=−\mathrm{4} \\ $$$$\Rightarrow\:\:{r}^{\mathrm{2}} −\frac{\mathrm{16}}{{r}^{\mathrm{2}} }=\mathrm{15} \\ $$$$\Rightarrow\:{r}^{\mathrm{2}} =\mathrm{16}\:,\:{m}=\pm\mathrm{1} \\ $$$$\Rightarrow\:\:{r}+{mi}=\pm\left(\mathrm{4}−{i}\right) \\ $$$${x}=\frac{−\mathrm{5}{i}\pm\left(\mathrm{4}−{i}\right)}{\mathrm{2}} \\ $$$${x}_{\mathrm{3}} =\mathrm{2}−\mathrm{3}{i}\:\:,\:\:{x}_{\mathrm{4}} =−\mathrm{2}−\mathrm{2}{i} \\ $$$${similarly}\:{for}\:{p}=\pm\mathrm{1} \\ $$$$\underset{−} {{Now}\:{for}\:{p}=\pm\mathrm{4}} \\ $$$${x}^{\mathrm{2}} \mp\mathrm{4}{x}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{21}\pm\mathrm{5}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{13}=\mathrm{0}\:\&\:{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{8}=\mathrm{0} \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} ,{x}_{\mathrm{2}} =\mathrm{2}\pm\mathrm{3}{i}\:\:\&\:\:{x}_{\mathrm{3}} ,{x}_{\mathrm{4}} =−\mathrm{2}\pm\mathrm{2}{i} \\ $$$$\left({fine}\:{formula}\:{i}\:{developed};\right. \\ $$$$\:\:{handles}\:{all}\:{biquadratics}\:{with} \\ $$$$\:\:{real}\:{coefficients}\:{real}\:{well}, \\ $$$$\left.\:\:{i}\:{dont}\:{just}\:{imagine}!\right) \\ $$

Commented by ajfour last updated on 05/Aug/19

$$\mathcal{I}{ts}\:{Time}\:{to}\:{try}\:{quintic}\:{again}. \\ $$

Commented by mr W last updated on 05/Aug/19

$${that}'{s}\:{great}! \\ $$

Commented by TawaTawa last updated on 05/Aug/19

$$\mathrm{This}\:\mathrm{is}\:\mathrm{great}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by TawaTawa last updated on 05/Aug/19

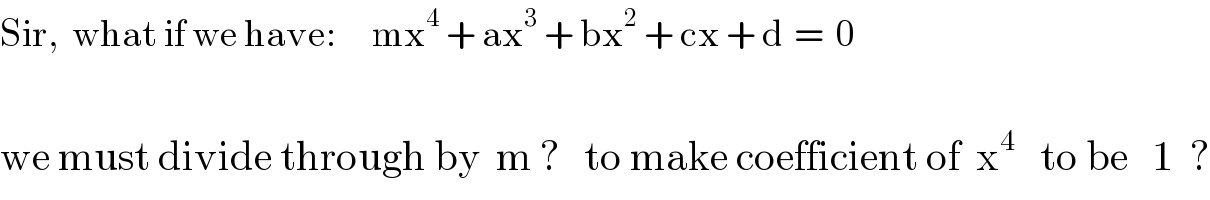
Sir, what if we have: mx^4 + ax^3 + bx^2 + cx + d = 0 we must divide through by m ? to make coefficient of x^4 to be 1 ?

$$\mathrm{Sir},\:\:\mathrm{what}\:\mathrm{if}\:\mathrm{we}\:\mathrm{have}:\:\:\:\:\:\:\mathrm{mx}^{\mathrm{4}} \:+\:\mathrm{ax}^{\mathrm{3}} \:+\:\mathrm{bx}^{\mathrm{2}} \:+\:\mathrm{cx}\:+\:\mathrm{d}\:\:=\:\:\mathrm{0} \\ $$$$ \\ $$$$\mathrm{we}\:\mathrm{must}\:\mathrm{divide}\:\mathrm{through}\:\mathrm{by}\:\:\mathrm{m}\:?\:\:\:\mathrm{to}\:\mathrm{make}\:\mathrm{coefficient}\:\mathrm{of}\:\:\mathrm{x}^{\mathrm{4}} \:\:\:\mathrm{to}\:\mathrm{be}\:\:\:\mathrm{1}\:\:? \\ $$

Commented by behi83417@gmail.com last updated on 05/Aug/19

nice method sir Ajfour.I love it. thanks for sharing this knowldege.

$$\mathrm{nice}\:\mathrm{method}\:\mathrm{sir}\:\mathrm{Ajfour}.\mathrm{I}\:\mathrm{love}\:\mathrm{it}. \\ $$$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{sharing}\:\mathrm{this}\:\mathrm{knowldege}. \\ $$

Commented by ajfour last updated on 05/Aug/19

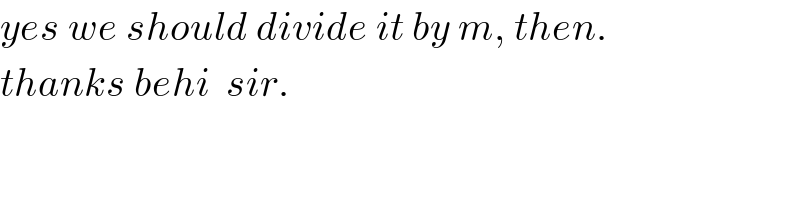
$${yes}\:{we}\:{should}\:{divide}\:{it}\:{by}\:{m},\:{then}. \\ $$$${thanks}\:{behi}\:\:{sir}. \\ $$

Commented by TawaTawa last updated on 05/Aug/19

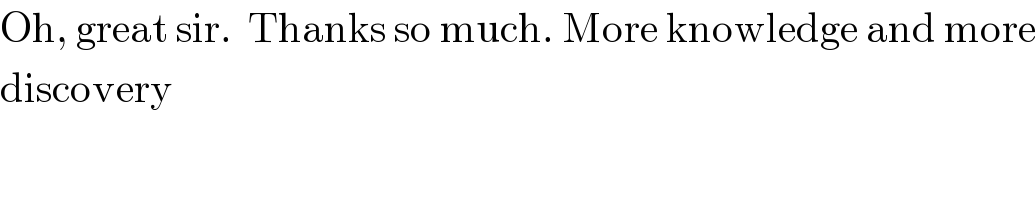
Oh, great sir. Thanks so much. More knowledge and more discovery

$$\mathrm{Oh},\:\mathrm{great}\:\mathrm{sir}.\:\:\mathrm{Thanks}\:\mathrm{so}\:\mathrm{much}.\:\mathrm{More}\:\mathrm{knowledge}\:\mathrm{and}\:\mathrm{more} \\ $$$$\mathrm{discovery} \\ $$

Commented by TawaTawa last updated on 05/Aug/19

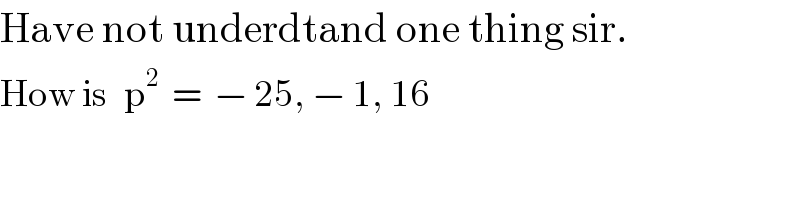
Have not underdtand one thing sir. How is p^2 = − 25, − 1, 16

$$\mathrm{Have}\:\mathrm{not}\:\mathrm{underdtand}\:\mathrm{one}\:\mathrm{thing}\:\mathrm{sir}. \\ $$$$\mathrm{How}\:\mathrm{is}\:\:\:\mathrm{p}^{\mathrm{2}} \:\:=\:\:−\:\mathrm{25},\:−\:\mathrm{1},\:\mathrm{16} \\ $$

Commented by ajfour last updated on 05/Aug/19

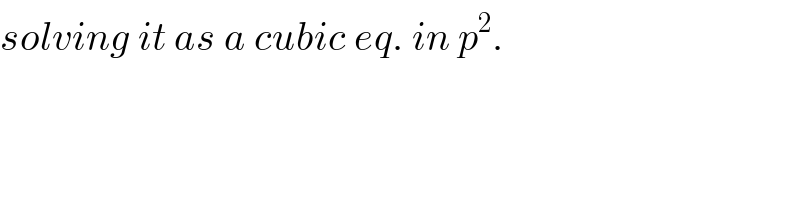
$${solving}\:{it}\:{as}\:{a}\:{cubic}\:{eq}.\:{in}\:{p}^{\mathrm{2}} . \\ $$

Commented by TawaTawa last updated on 05/Aug/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by ajfour last updated on 05/Aug/19

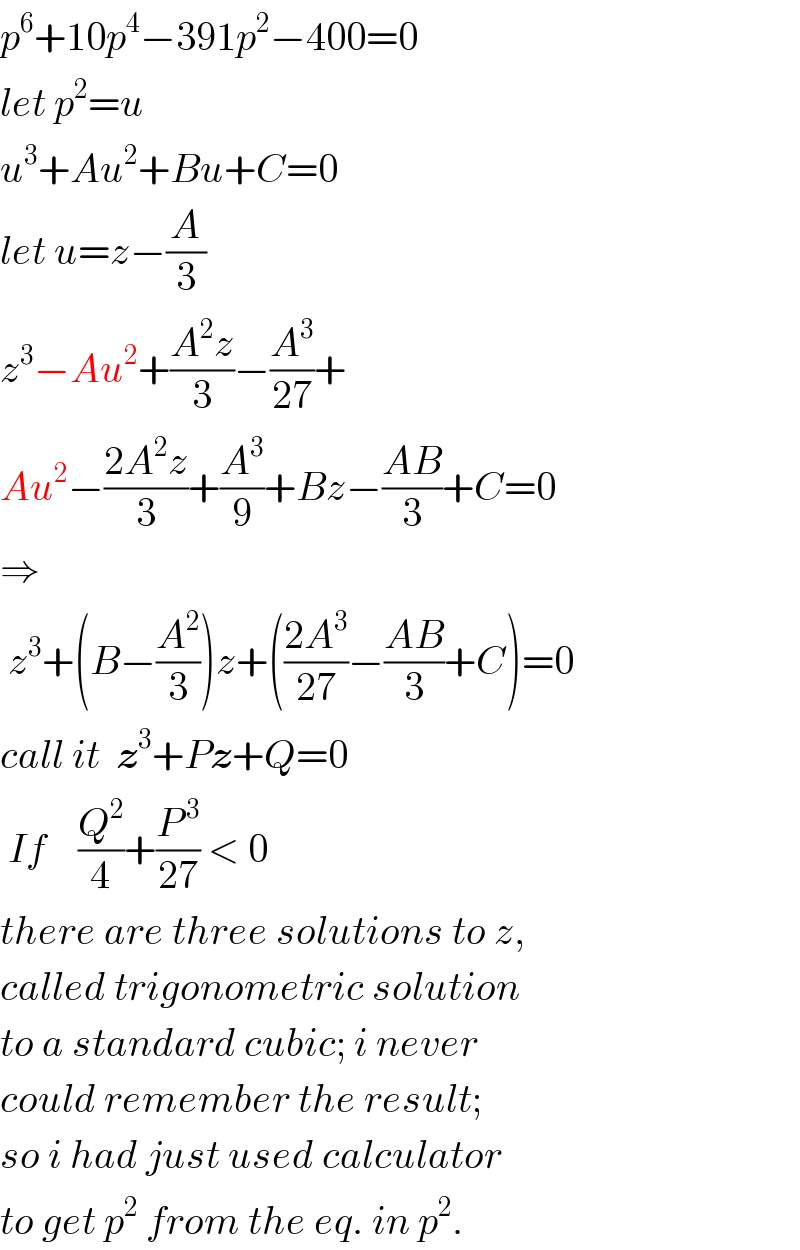
p^6 +10p^4 −391p^2 −400=0 let p^2 =u u^3 +Au^2 +Bu+C=0 let u=z−(A/3) z^3 −Au^2 +((A^2 z)/3)−(A^3 /(27))+ Au^2 −((2A^2 z)/3)+(A^3 /9)+Bz−((AB)/3)+C=0 ⇒ z^3 +(B−(A^2 /3))z+(((2A^3 )/(27))−((AB)/3)+C)=0 call it z^3 +Pz+Q=0 If (Q^2 /4)+(P^( 3) /(27)) < 0 there are three solutions to z, called trigonometric solution to a standard cubic; i never could remember the result; so i had just used calculator to get p^2 from the eq. in p^2 .

$${p}^{\mathrm{6}} +\mathrm{10}{p}^{\mathrm{4}} −\mathrm{391}{p}^{\mathrm{2}} −\mathrm{400}=\mathrm{0} \\ $$$${let}\:{p}^{\mathrm{2}} ={u} \\ $$$${u}^{\mathrm{3}} +{Au}^{\mathrm{2}} +{Bu}+{C}=\mathrm{0} \\ $$$${let}\:{u}={z}−\frac{{A}}{\mathrm{3}} \\ $$$${z}^{\mathrm{3}} −{Au}^{\mathrm{2}} +\frac{{A}^{\mathrm{2}} {z}}{\mathrm{3}}−\frac{{A}^{\mathrm{3}} }{\mathrm{27}}+ \\ $$$${Au}^{\mathrm{2}} −\frac{\mathrm{2}{A}^{\mathrm{2}} {z}}{\mathrm{3}}+\frac{{A}^{\mathrm{3}} }{\mathrm{9}}+{Bz}−\frac{{AB}}{\mathrm{3}}+{C}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\:{z}^{\mathrm{3}} +\left({B}−\frac{{A}^{\mathrm{2}} }{\mathrm{3}}\right){z}+\left(\frac{\mathrm{2}{A}^{\mathrm{3}} }{\mathrm{27}}−\frac{{AB}}{\mathrm{3}}+{C}\right)=\mathrm{0} \\ $$$${call}\:{it}\:\:\boldsymbol{{z}}^{\mathrm{3}} +{P}\boldsymbol{{z}}+{Q}=\mathrm{0} \\ $$$$\:{If}\:\:\:\:\frac{{Q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{P}^{\:\mathrm{3}} }{\mathrm{27}}\:<\:\mathrm{0} \\ $$$${there}\:{are}\:{three}\:{solutions}\:{to}\:{z}, \\ $$$${called}\:{trigonometric}\:{solution} \\ $$$${to}\:{a}\:{standard}\:{cubic};\:{i}\:{never} \\ $$$${could}\:{remember}\:{the}\:{result}; \\ $$$${so}\:{i}\:{had}\:{just}\:{used}\:{calculator} \\ $$$${to}\:{get}\:{p}^{\mathrm{2}} \:{from}\:{the}\:{eq}.\:{in}\:{p}^{\mathrm{2}} . \\ $$

Commented by TawaTawa last updated on 05/Aug/19

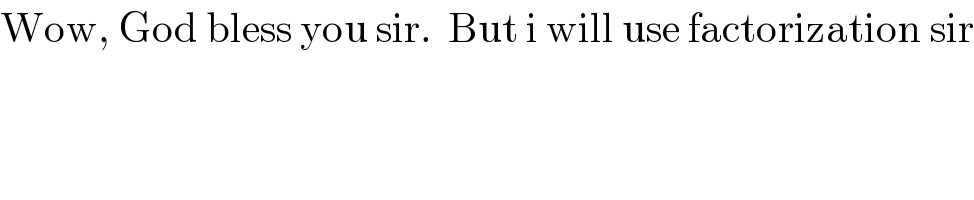
Wow, God bless you sir. But i will use factorization sir

$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{But}\:\mathrm{i}\:\mathrm{will}\:\mathrm{use}\:\mathrm{factorization}\:\mathrm{sir} \\ $$

Commented by TawaTawa last updated on 05/Aug/19

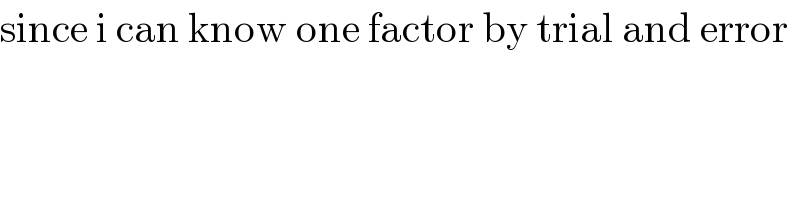
since i can know one factor by trial and error

$$\mathrm{since}\:\mathrm{i}\:\mathrm{can}\:\mathrm{know}\:\mathrm{one}\:\mathrm{factor}\:\mathrm{by}\:\mathrm{trial}\:\mathrm{and}\:\mathrm{error} \\ $$

Commented by TawaTawa last updated on 05/Aug/19

or i can use sir MrW formular posted on cubic equation

$$\mathrm{or}\:\mathrm{i}\:\mathrm{can}\:\mathrm{use}\:\mathrm{sir}\:\:\mathrm{MrW}\:\:\mathrm{formular}\:\mathrm{posted}\:\mathrm{on}\:\mathrm{cubic}\:\mathrm{equation} \\ $$

Commented by TawaTawa last updated on 05/Aug/19

Sir, in the equation, no term in x^3 . it means the method cannot work for ax^4 + bx^3 + cx^2 + dx + e = 0 except ax^4 + bx^2 + cx + d = 0 just want to know sir.

$$\mathrm{Sir},\:\mathrm{in}\:\mathrm{the}\:\mathrm{equation},\:\:\mathrm{no}\:\mathrm{term}\:\mathrm{in}\:\:\:\:\mathrm{x}^{\mathrm{3}} .\:\:\:\mathrm{it}\:\mathrm{means}\:\mathrm{the}\:\mathrm{method}\:\mathrm{cannot} \\ $$$$\mathrm{work}\:\mathrm{for}\:\:\:\:\:\mathrm{ax}^{\mathrm{4}} \:+\:\mathrm{bx}^{\mathrm{3}} \:+\:\mathrm{cx}^{\mathrm{2}} \:+\:\mathrm{dx}\:+\:\mathrm{e}\:\:=\:\:\mathrm{0}\:\:\:\:\:\mathrm{except}\:\:\:\:\mathrm{ax}^{\mathrm{4}} \:+\:\mathrm{bx}^{\mathrm{2}} \:+\:\mathrm{cx}\:+\:\mathrm{d}\:=\:\mathrm{0} \\ $$$$\mathrm{just}\:\mathrm{want}\:\mathrm{to}\:\mathrm{know}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 05/Aug/19

eqn. with x^3 term can be transformed to an eqn. without x^3 term using a simple substitution x=t−(a/4) where a is the coefficient of x^3 term. see Q65830.

$${eqn}.\:{with}\:{x}^{\mathrm{3}} \:{term}\:{can}\:{be}\:{transformed} \\ $$$${to}\:{an}\:{eqn}.\:{without}\:{x}^{\mathrm{3}} \:{term}\:{using}\:{a}\:{simple} \\ $$$${substitution}\:{x}={t}−\frac{{a}}{\mathrm{4}}\:{where}\:{a}\:{is}\:{the} \\ $$$${coefficient}\:{of}\:{x}^{\mathrm{3}} \:{term}.\:{see}\:{Q}\mathrm{65830}. \\ $$

Commented by TawaTawa last updated on 05/Aug/19

Just checked now sir. God bless you sir. i now understand all

$$\mathrm{Just}\:\mathrm{checked}\:\mathrm{now}\:\mathrm{sir}.\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{i}\:\mathrm{now}\:\mathrm{understand}\:\mathrm{all} \\ $$

Facebook Tweet Pin