x-5-x-3-1-1-3-dx-

Question Number 11149 by suci last updated on 14/Mar/17

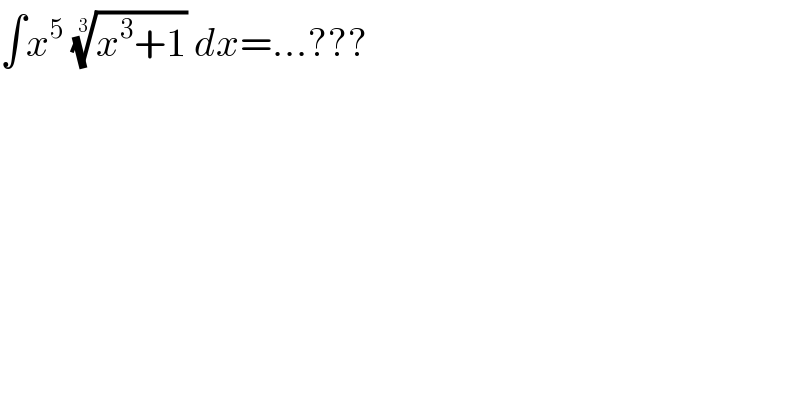
$$\int{x}^{\mathrm{5}} \:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +\mathrm{1}}\:{dx}=…??? \\ $$

Answered by ajfour last updated on 14/Mar/17

(((x^3 +1)^(7/3) )/7)−(((x^3 +1)^(4/3) )/4) +C

$$\:\frac{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{7}/\mathrm{3}} }{\mathrm{7}}−\frac{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{4}/\mathrm{3}} }{\mathrm{4}}\:+{C}\: \\ $$

Commented by ajfour last updated on 14/Mar/17

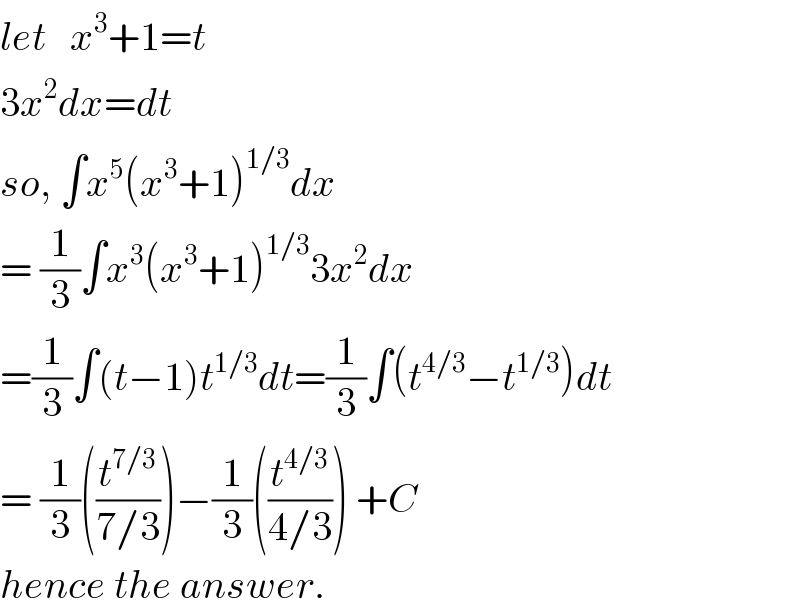
let x^3 +1=t 3x^2 dx=dt so, ∫x^5 (x^3 +1)^(1/3) dx = (1/3)∫x^3 (x^3 +1)^(1/3) 3x^2 dx =(1/3)∫(t−1)t^(1/3) dt=(1/3)∫(t^(4/3) −t^(1/3) )dt = (1/3)((t^(7/3) /(7/3)))−(1/3)((t^(4/3) /(4/3))) +C hence the answer.

$${let}\:\:\:{x}^{\mathrm{3}} +\mathrm{1}={t} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} {dx}={dt} \\ $$$${so},\:\int{x}^{\mathrm{5}} \left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} {dx}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}\int{x}^{\mathrm{3}} \left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} \mathrm{3}{x}^{\mathrm{2}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\left({t}−\mathrm{1}\right){t}^{\mathrm{1}/\mathrm{3}} {dt}=\frac{\mathrm{1}}{\mathrm{3}}\int\left({t}^{\mathrm{4}/\mathrm{3}} −{t}^{\mathrm{1}/\mathrm{3}} \right){dt} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{t}^{\mathrm{7}/\mathrm{3}} }{\mathrm{7}/\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{t}^{\mathrm{4}/\mathrm{3}} }{\mathrm{4}/\mathrm{3}}\right)\:+{C} \\ $$$${hence}\:{the}\:{answer}. \\ $$

Answered by Mechas88 last updated on 17/Mar/17

u=(x^3 +1)^(1/3) u^3 =x^3 +1 x^3 =u^3 −1 du=(1/3)(x^3 +1)^(−2/3) (3x^2 )dx=x^2 (x^3 +1)^(−2/3) dx dx=x^(−2) (x^3 +1)^(2/3) du ∫x^5 x^(−2) udu=∫(u^3 −1)udu= ∫u^4 du−∫udu= (u^5 /5) − (u^2 /2) + C= (((((x^3 +1)^5 ))^(1/3) )/5) −((((x^3 +1)^2 ))^(1/3) /2) + C ∗∗∗Rta

$$ \\ $$$${u}=\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$${u}^{\mathrm{3}} ={x}^{\mathrm{3}} +\mathrm{1} \\ $$$${x}^{\mathrm{3}} ={u}^{\mathrm{3}} −\mathrm{1} \\ $$$${du}=\frac{\mathrm{1}}{\mathrm{3}}\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{−\mathrm{2}/\mathrm{3}} \left(\mathrm{3}{x}^{\mathrm{2}} \right){dx}={x}^{\mathrm{2}} \left({x}^{\mathrm{3}} +\mathrm{1}\right)^{−\mathrm{2}/\mathrm{3}} {dx} \\ $$$${dx}={x}^{−\mathrm{2}} \left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}/\mathrm{3}} {du} \\ $$$$ \\ $$$$\int{x}^{\mathrm{5}} {x}^{−\mathrm{2}} {udu}=\int\left({u}^{\mathrm{3}} −\mathrm{1}\right){udu}= \\ $$$$\int{u}^{\mathrm{4}} {du}−\int{udu}= \\ $$$$\frac{{u}^{\mathrm{5}} }{\mathrm{5}}\:−\:\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:+\:{C}= \\ $$$$\frac{\sqrt[{\mathrm{3}}]{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{5}} }\:}{\mathrm{5}}\:−\frac{\sqrt[{\mathrm{3}}]{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} \:\:\:\:}}{\mathrm{2}}\:\:+\:\:{C}\:\:\ast\ast\ast{Rta} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply