Question Number 11982 by tawa last updated on 08/Apr/17
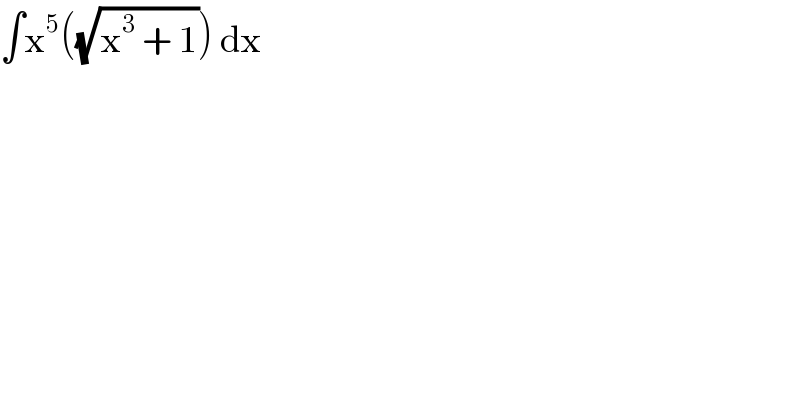
$$\int\mathrm{x}^{\mathrm{5}} \left(\sqrt{\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{1}}\right)\:\mathrm{dx} \\ $$
Answered by ajfour last updated on 08/Apr/17
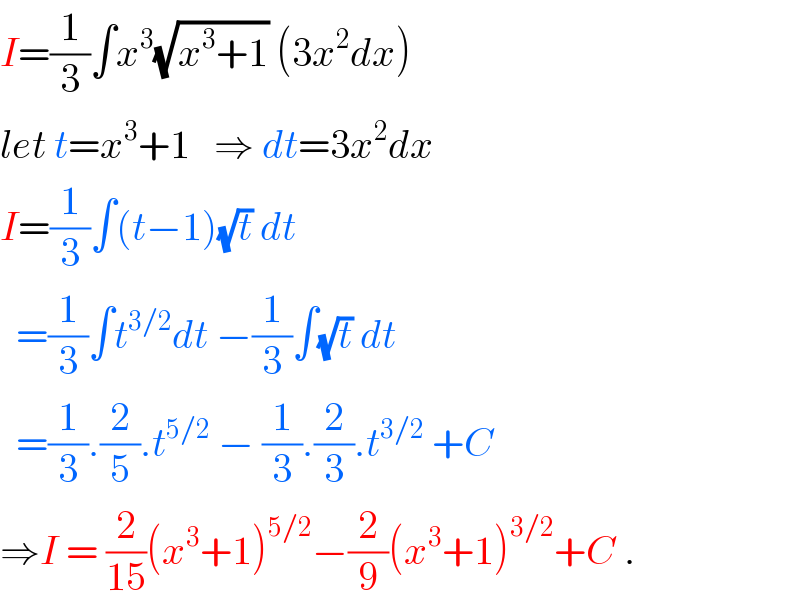
$${I}=\frac{\mathrm{1}}{\mathrm{3}}\int{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:\left(\mathrm{3}{x}^{\mathrm{2}} {dx}\right) \\ $$$${let}\:{t}={x}^{\mathrm{3}} +\mathrm{1}\:\:\:\Rightarrow\:{dt}=\mathrm{3}{x}^{\mathrm{2}} {dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{3}}\int\left({t}−\mathrm{1}\right)\sqrt{{t}}\:{dt} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}\int{t}^{\mathrm{3}/\mathrm{2}} {dt}\:−\frac{\mathrm{1}}{\mathrm{3}}\int\sqrt{{t}}\:{dt} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{2}}{\mathrm{5}}.{t}^{\mathrm{5}/\mathrm{2}} \:−\:\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{2}}{\mathrm{3}}.{t}^{\mathrm{3}/\mathrm{2}} \:+{C} \\ $$$$\Rightarrow{I}\:=\:\frac{\mathrm{2}}{\mathrm{15}}\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{5}/\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{9}}\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} +{C}\:. \\ $$
Commented by tawa last updated on 08/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
