Menu Close

x-6-1-x-3-1-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 138909 by bramlexs22 last updated on 19/Apr/21
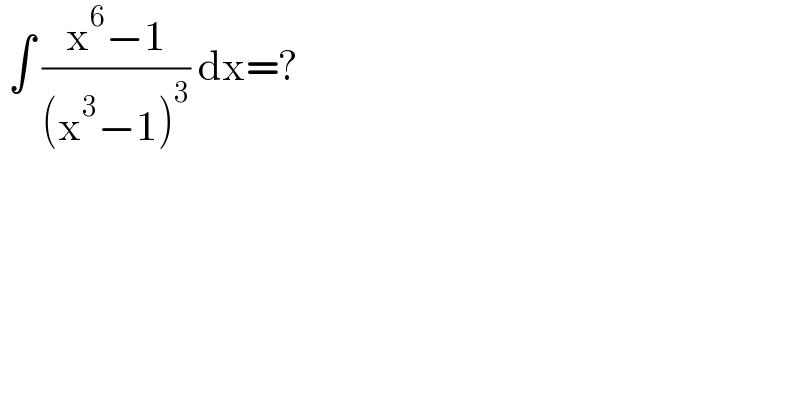
∫ ((x^6 −1)/((x^3 −1)^3 )) dx=?
$$\:\int\:\frac{\mathrm{x}^{\mathrm{6}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{3}} }\:\mathrm{dx}=? \\ $$
Answered by mathmax by abdo last updated on 20/Apr/21
Φ=∫ ((x^6 −1)/((x^3 −1)^3 ))dx⇒Φ=∫ ((x^6 −1)/((x−1)^3 (x^2 +x+1)^3 ))dx the roots of x^2 +x+1=are j=e^((i2π)/3) and j^− =e^(−((i2π)/3)) ⇒ Φ=∫ ((x^6 −1)/((x−1)^3 (x−j)^3 (x−j^− )^3 ))dx =∫ ((x^6 −1)/((x−1)^3 (((x−j)/(x−j^− )))^3 (x−j^− )^6 ))dx we do the changement ((x−j)/(x−j^− ))=t ⇒x−j=tx−j^− t ⇒ (1−t)x=j−j^− t ⇒x=((j−j^− t)/(1−t)) ⇒(dx/dt)=((−j^− (1−t)−(j−j^− t)(−1))/((1−t)^2 )) =((j−j^− )/((1−t)^2 )) =((2i.((√3)/2))/((1−t)^2 )) =((i(√3))/(2(1−t)^2 )) and x−j^− =((j−j^− t)/(1−t))−j^− =((j−j^− t−j^− +j^− t)/(1−t))=((i(√3))/(2(1−t))) also x−1=((j−j^− t)/(1−t))−1 =((j−j^− t−1+t)/(1−t)) =((j−1+(1−j^− )t)/(1−t)) ⇒ Φ =∫ (((((j−j^− t)/(1−t)))^6 −1)/((((j−1+(1−j^− )t)/(1−t)))^3 t^3 (((i(√3))/(2(1−t))))^6 ))((i(√3))/(2(1−t)^2 ))dt =∫ (((((j−j^− t)/(1−t)))^6 −1)(1−t)^9 .2^6 (i(√3)))/((j−1+(1−j^− )t)^3 t^3 .2.(i(√3))^6 (1−t)^2 ))dt =(2^5 /((i(√3))^5 ))∫ (({(((j−j^− t)/(1−t)))^6 −1}(1−t)^7 )/(t^3 (j−1+(1−j^− )t)^3 ))dt =((2/(i(√3))))^5 ∫ (((1−t)(j−j^− t)^6 −(1−t)^7 )/(t^3 (j−1+(1−j^− t))^3 ))dt =((2/(i(√3))))^5 ∫ (((1−t)(j−j^− t)^6 )/(t^3 (j−1+(1−j^− t))^3 ))dt−((2/(i(√3))))^5 ∫ (((1−t)^7 )/(t^3 (j−1+(1−j^− t)^3 ))dt ....be continued....
$$\Phi=\int\:\:\frac{\mathrm{x}^{\mathrm{6}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dx}\Rightarrow\Phi=\int\:\:\frac{\mathrm{x}^{\mathrm{6}} −\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dx} \\ $$$$\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}=\mathrm{are}\:\mathrm{j}=\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:\mathrm{and}\:\overset{−} {\mathrm{j}}=\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:\Rightarrow \\ $$$$\Phi=\int\:\:\frac{\mathrm{x}^{\mathrm{6}} −\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}−\mathrm{j}\right)^{\mathrm{3}} \left(\mathrm{x}−\overset{−} {\mathrm{j}}\right)^{\mathrm{3}} }\mathrm{dx}\:=\int\:\:\frac{\mathrm{x}^{\mathrm{6}} −\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} \left(\frac{\mathrm{x}−\mathrm{j}}{\mathrm{x}−\overset{−} {\mathrm{j}}}\right)^{\mathrm{3}} \left(\mathrm{x}−\overset{−} {\mathrm{j}}\right)^{\mathrm{6}} }\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{x}−\mathrm{j}}{\mathrm{x}−\overset{−} {\mathrm{j}}}=\mathrm{t}\:\Rightarrow\mathrm{x}−\mathrm{j}=\mathrm{tx}−\overset{−} {\mathrm{j}t}\:\Rightarrow \\ $$$$\left(\mathrm{1}−\mathrm{t}\right)\mathrm{x}=\mathrm{j}−\overset{−} {\mathrm{j}t}\:\Rightarrow\mathrm{x}=\frac{\mathrm{j}−\overset{−} {\mathrm{j}t}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{−\overset{−} {\mathrm{j}}\left(\mathrm{1}−\mathrm{t}\right)−\left(\mathrm{j}−\overset{−} {\mathrm{j}t}\right)\left(−\mathrm{1}\right)}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{j}−\overset{−} {\mathrm{j}}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2i}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\:=\frac{\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\:\mathrm{and}\:\mathrm{x}−\overset{−} {\mathrm{j}}=\frac{\mathrm{j}−\overset{−} {\mathrm{j}t}}{\mathrm{1}−\mathrm{t}}−\overset{−} {\mathrm{j}} \\ $$$$=\frac{\mathrm{j}−\overset{−} {\mathrm{j}t}−\overset{−} {\mathrm{j}}+\overset{−} {\mathrm{j}t}}{\mathrm{1}−\mathrm{t}}=\frac{\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}\left(\mathrm{1}−\mathrm{t}\right)}\:\mathrm{also}\:\mathrm{x}−\mathrm{1}=\frac{\mathrm{j}−\overset{−} {\mathrm{j}t}}{\mathrm{1}−\mathrm{t}}−\mathrm{1} \\ $$$$=\frac{\mathrm{j}−\overset{−} {\mathrm{j}t}−\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}\:=\frac{\mathrm{j}−\mathrm{1}+\left(\mathrm{1}−\overset{−} {\mathrm{j}}\right)\mathrm{t}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow \\ $$$$\Phi\:=\int\:\:\:\frac{\left(\frac{\mathrm{j}−\overset{−} {\mathrm{j}t}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{6}} −\mathrm{1}}{\left(\frac{\mathrm{j}−\mathrm{1}+\left(\mathrm{1}−\overset{−} {\mathrm{j}}\right)\mathrm{t}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{3}} \:\mathrm{t}^{\mathrm{3}} \left(\frac{\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}\left(\mathrm{1}−\mathrm{t}\right)}\right)^{\mathrm{6}} }\frac{\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\int\:\:\:\:\frac{\left.\left(\frac{\mathrm{j}−\overset{−} {\mathrm{j}t}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{6}} −\mathrm{1}\right)\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{9}} .\mathrm{2}^{\mathrm{6}} \:\left(\mathrm{i}\sqrt{\mathrm{3}}\right)}{\left(\mathrm{j}−\mathrm{1}+\left(\mathrm{1}−\overset{−} {\mathrm{j}}\right)\mathrm{t}\right)^{\mathrm{3}} \mathrm{t}^{\mathrm{3}} \:.\mathrm{2}.\left(\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{6}} \left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{2}^{\mathrm{5}} }{\left(\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{5}} }\int\:\:\frac{\left\{\left(\frac{\mathrm{j}−\overset{−} {\mathrm{j}t}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{6}} −\mathrm{1}\right\}\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{7}} }{\mathrm{t}^{\mathrm{3}} \left(\mathrm{j}−\mathrm{1}+\left(\mathrm{1}−\overset{−} {\mathrm{j}}\right)\mathrm{t}\right)^{\mathrm{3}} }\mathrm{dt} \\ $$$$=\left(\frac{\mathrm{2}}{\mathrm{i}\sqrt{\mathrm{3}}}\right)^{\mathrm{5}} \:\int\:\:\:\frac{\left(\mathrm{1}−\mathrm{t}\right)\left(\mathrm{j}−\overset{−} {\mathrm{j}t}\right)^{\mathrm{6}} −\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{7}} }{\mathrm{t}^{\mathrm{3}} \left(\mathrm{j}−\mathrm{1}+\left(\mathrm{1}−\overset{−} {\mathrm{j}t}\right)\right)^{\mathrm{3}} }\mathrm{dt} \\ $$$$=\left(\frac{\mathrm{2}}{\mathrm{i}\sqrt{\mathrm{3}}}\right)^{\mathrm{5}} \:\int\:\:\frac{\left(\mathrm{1}−\mathrm{t}\right)\left(\mathrm{j}−\overset{−} {\mathrm{j}t}\right)^{\mathrm{6}} }{\mathrm{t}^{\mathrm{3}} \left(\mathrm{j}−\mathrm{1}+\left(\mathrm{1}−\overset{−} {\mathrm{j}t}\right)\right)^{\mathrm{3}} }\mathrm{dt}−\left(\frac{\mathrm{2}}{\mathrm{i}\sqrt{\mathrm{3}}}\right)^{\mathrm{5}} \int\:\frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{7}} }{\mathrm{t}^{\mathrm{3}} \left(\mathrm{j}−\mathrm{1}+\left(\mathrm{1}−\overset{−} {\mathrm{j}t}\right)^{\mathrm{3}} \right.}\mathrm{dt} \\ $$$$….\mathrm{be}\:\mathrm{continued}…. \\ $$
Answered by phanphuoc last updated on 20/Apr/21
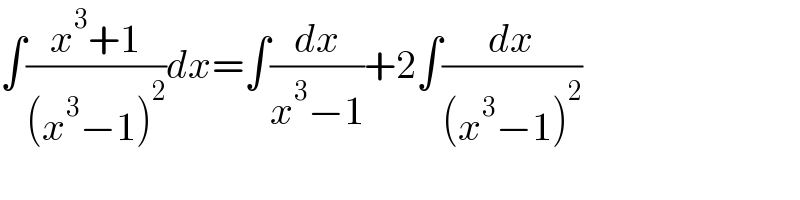
∫((x^3 +1)/((x^3 −1)^2 ))dx=∫(dx/(x^3 −1))+2∫(dx/((x^3 −1)^2 ))
$$\int\frac{{x}^{\mathrm{3}} +\mathrm{1}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }{dx}=\int\frac{{dx}}{{x}^{\mathrm{3}} −\mathrm{1}}+\mathrm{2}\int\frac{{dx}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Answered by MJS_new last updated on 20/Apr/21
∫(((x^3 −1)(x^3 +1))/((x^3 −1)^3 ))dx=∫((x^3 +1)/((x^3 −1)^2 ))dx= [Ostrogradski′s Method] =−((2x)/(3(x^3 −1)))−(1/3)∫(dx/(x^3 −1))= =−((2x)/(3(x^3 −1)))+(1/9)∫((x+2)/(x^2 +x+1))dx−(1/9)∫(dx/(x−1))= =−((2x)/(3(x^3 −1)))+((√3)/9)arctan ((2x+1)/( (√3))) +(1/(18))ln (x^2 +x+1) −(1/9)ln ∣x−1∣ +C
$$\int\frac{\left({x}^{\mathrm{3}} −\mathrm{1}\right)\left({x}^{\mathrm{3}} +\mathrm{1}\right)}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{3}} }{dx}=\int\frac{{x}^{\mathrm{3}} +\mathrm{1}}{\left({x}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=−\frac{\mathrm{2}{x}}{\mathrm{3}\left({x}^{\mathrm{3}} −\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}^{\mathrm{3}} −\mathrm{1}}= \\ $$$$=−\frac{\mathrm{2}{x}}{\mathrm{3}\left({x}^{\mathrm{3}} −\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{9}}\int\frac{{x}+\mathrm{2}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}−\frac{\mathrm{1}}{\mathrm{9}}\int\frac{{dx}}{{x}−\mathrm{1}}= \\ $$$$=−\frac{\mathrm{2}{x}}{\mathrm{3}\left({x}^{\mathrm{3}} −\mathrm{1}\right)}+\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:+\frac{\mathrm{1}}{\mathrm{18}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\:−\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\mid{x}−\mathrm{1}\mid\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *