Question Number 7872 by tawakalitu last updated on 22/Sep/16
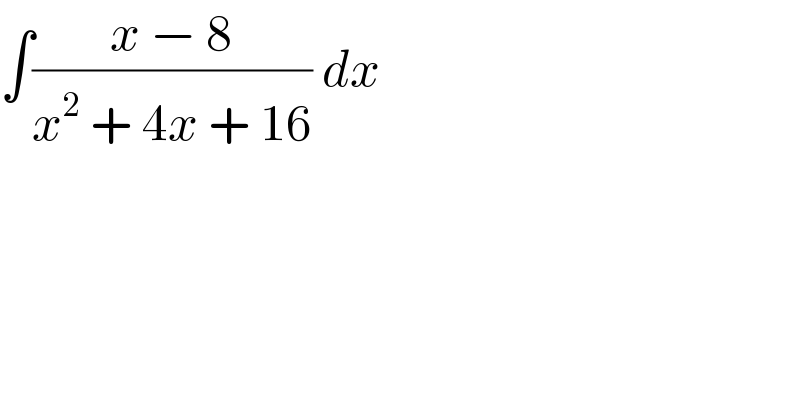
$$\int\frac{{x}\:−\:\mathrm{8}}{{x}^{\mathrm{2}} \:+\:\mathrm{4}{x}\:+\:\mathrm{16}}\:{dx} \\ $$
Commented by prakash jain last updated on 23/Sep/16

$$\frac{{x}−\mathrm{8}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{16}}=\frac{{x}−\mathrm{8}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}+\mathrm{12}} \\ $$$$=\frac{{x}−\mathrm{8}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} −\left({i}\sqrt{\mathrm{12}}\right)^{\mathrm{2}} } \\ $$$$=\frac{{x}−\mathrm{8}}{\left({x}+\mathrm{2}+{i}\sqrt{\mathrm{12}}\right)\left({x}+\mathrm{2}−{i}\sqrt{\mathrm{12}}\right)} \\ $$$${convert}\:{to}\:{partial}\:{fraction}\: \\ $$$$\left({x}−\mathrm{8}\right)\left(\frac{\mathrm{1}}{{x}+\mathrm{2}−{i}\sqrt{\mathrm{12}}}−\frac{\mathrm{1}}{{x}+\mathrm{2}+{i}\sqrt{\mathrm{12}}}\right)\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{12}}} \\ $$$$\left(\frac{{x}−\mathrm{8}}{{x}−\mathrm{2}−{i}\sqrt{\mathrm{12}}}−\frac{{x}−\mathrm{8}}{{x}−\mathrm{2}+{i}\sqrt{\mathrm{12}}}\right)\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{12}}} \\ $$$$\left(\frac{{x}+\mathrm{2}−{i}\sqrt{\mathrm{12}}−\left(\mathrm{10}−{i}\sqrt{\mathrm{12}}\right)}{{x}+\mathrm{2}−{i}\sqrt{\mathrm{12}}}−\frac{{x}+\mathrm{2}+{i}\sqrt{\mathrm{12}}−\left(\mathrm{10}+{i}\sqrt{\mathrm{12}}\right)}{{x}+\mathrm{2}+{i}\sqrt{\mathrm{12}}}\right)\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{12}}} \\ $$$$\left(\frac{\left(\mathrm{10}−{i}\sqrt{\mathrm{12}}\right)}{{x}−\mathrm{2}−{i}\sqrt{\mathrm{12}}}−\frac{\left(\mathrm{10}+{i}\sqrt{\mathrm{12}}\right)}{{x}−\mathrm{2}+{i}\sqrt{\mathrm{12}}}\right)\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{12}}} \\ $$$$ \\ $$
Commented by tawakalitu last updated on 22/Sep/16

$${Thanks}\:{so}\:{much} \\ $$
Commented by sandy_suhendra last updated on 23/Sep/16
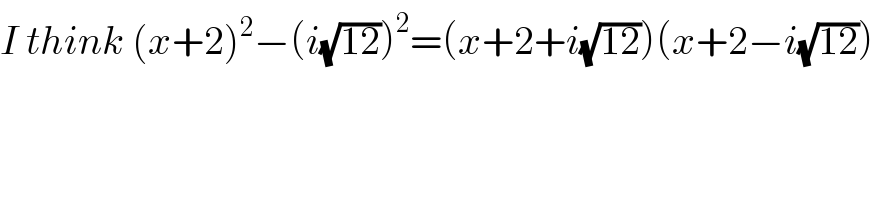
$${I}\:{think}\:\left({x}+\mathrm{2}\right)^{\mathrm{2}} −\left({i}\sqrt{\mathrm{12}}\right)^{\mathrm{2}} =\left({x}+\mathrm{2}+{i}\sqrt{\mathrm{12}}\right)\left({x}+\mathrm{2}−{i}\sqrt{\mathrm{12}}\right) \\ $$
Commented by prakash jain last updated on 23/Sep/16

$$\mathrm{Thanks} \\ $$
Answered by prakash jain last updated on 02/Oct/16

$$\mathrm{see}\:\mathrm{comments} \\ $$
