Question Number 1016 by 123456 last updated on 14/May/15
![[(x^→ ×a^→ )×b^→ ]×x^→ =c^→](https://www.tinkutara.com/question/Q1016.png)
$$\left[\left(\overset{\rightarrow} {{x}}×\overset{\rightarrow} {{a}}\right)×\overset{\rightarrow} {{b}}\right]×\overset{\rightarrow} {{x}}=\overset{\rightarrow} {{c}} \\ $$
Answered by rpatle69@gmail.com last updated on 14/May/15
![[−b^→ ×(x^→ ×a^→ )]×x^→ =c^→ x^→ ×[b^→ ×(x^→ ×a^→ )]=c^→ x^→ ×[(b^→ .a^→ )x^→ −(b^→ .x^→ )a^→ ]=c^→](https://www.tinkutara.com/question/Q1017.png)
$$\left[−\overset{\rightarrow} {{b}}×\left(\overset{\rightarrow} {{x}}\:×\overset{\rightarrow} {{a}}\right)\right]×\overset{\rightarrow} {{x}}=\overset{\rightarrow} {{c}} \\ $$$$\overset{\rightarrow} {{x}}×\left[\overset{\rightarrow} {{b}}×\left(\overset{\rightarrow} {{x}}×\overset{\rightarrow} {{a}}\right)\right]=\overset{\rightarrow} {{c}} \\ $$$$\overset{\rightarrow} {{x}}×\left[\left(\overset{\rightarrow} {{b}}.\overset{\rightarrow} {{a}}\right)\overset{\rightarrow} {{x}}−\left(\overset{\rightarrow} {{b}}.\overset{\rightarrow} {{x}}\right)\overset{\rightarrow} {{a}}\right]=\overset{\rightarrow} {{c}} \\ $$$$ \\ $$$$ \\ $$
Commented by prakash jain last updated on 17/May/15
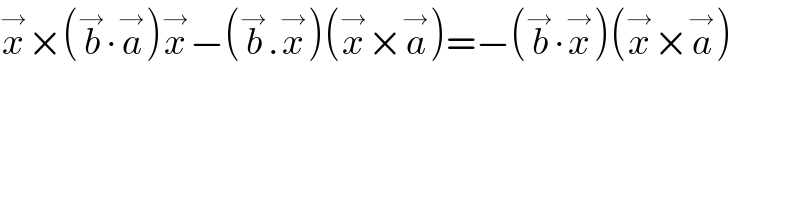
$$\overset{\rightarrow} {{x}}×\left(\overset{\rightarrow} {{b}}\centerdot\overset{\rightarrow} {{a}}\right)\overset{\rightarrow} {{x}}−\left(\overset{\rightarrow} {{b}}.\overset{\rightarrow} {{x}}\right)\left(\overset{\rightarrow} {{x}}×\overset{\rightarrow} {{a}}\right)=−\left(\overset{\rightarrow} {{b}}\centerdot\overset{\rightarrow} {{x}}\right)\left(\overset{\rightarrow} {{x}}×\overset{\rightarrow} {{a}}\right) \\ $$
Commented by 123456 last updated on 17/May/15
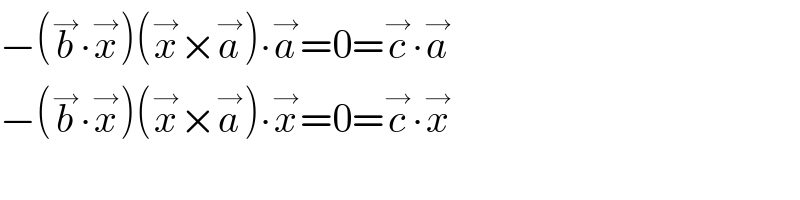
$$−\left(\overset{\rightarrow} {{b}}\centerdot\overset{\rightarrow} {{x}}\right)\left(\overset{\rightarrow} {{x}}×\overset{\rightarrow} {{a}}\right)\centerdot\overset{\rightarrow} {{a}}=\mathrm{0}=\overset{\rightarrow} {{c}}\centerdot\overset{\rightarrow} {{a}} \\ $$$$−\left(\overset{\rightarrow} {{b}}\centerdot\overset{\rightarrow} {{x}}\right)\left(\overset{\rightarrow} {{x}}×\overset{\rightarrow} {{a}}\right)\centerdot\overset{\rightarrow} {{x}}=\mathrm{0}=\overset{\rightarrow} {{c}}\centerdot\overset{\rightarrow} {{x}} \\ $$
Commented by 123456 last updated on 17/May/15
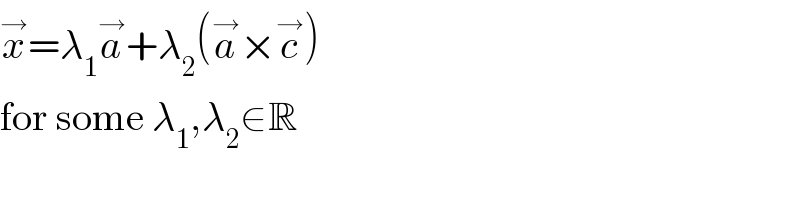
$$\overset{\rightarrow} {{x}}=\lambda_{\mathrm{1}} \overset{\rightarrow} {{a}}+\lambda_{\mathrm{2}} \left(\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{c}}\right) \\ $$$$\mathrm{for}\:\mathrm{some}\:\lambda_{\mathrm{1}} ,\lambda_{\mathrm{2}} \in\mathbb{R} \\ $$
