Question Number 73027 by mathmax by abdo last updated on 05/Nov/19

$${x}\:{and}\:{y}\:{are}\:{reals}\left({or}\:{complex}\right)\:{let}\:{put}\:{x}^{\left(\mathrm{0}\right)} =\mathrm{1}\:,{x}^{\left(\mathrm{1}\right)} ={x} \\ $$$${x}^{\left(\mathrm{2}\right)} ={x}\left({x}−\mathrm{1}\right)…..{x}^{\left({n}\right)} ={x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)…\left({x}−{n}+\mathrm{1}\right){prove}\:{that} \\ $$$$\left({x}+{y}\right)^{\left({n}\right)} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:{x}^{\left({n}−{k}\right)} {y}^{\left({k}\right)} \\ $$
Answered by mind is power last updated on 05/Nov/19
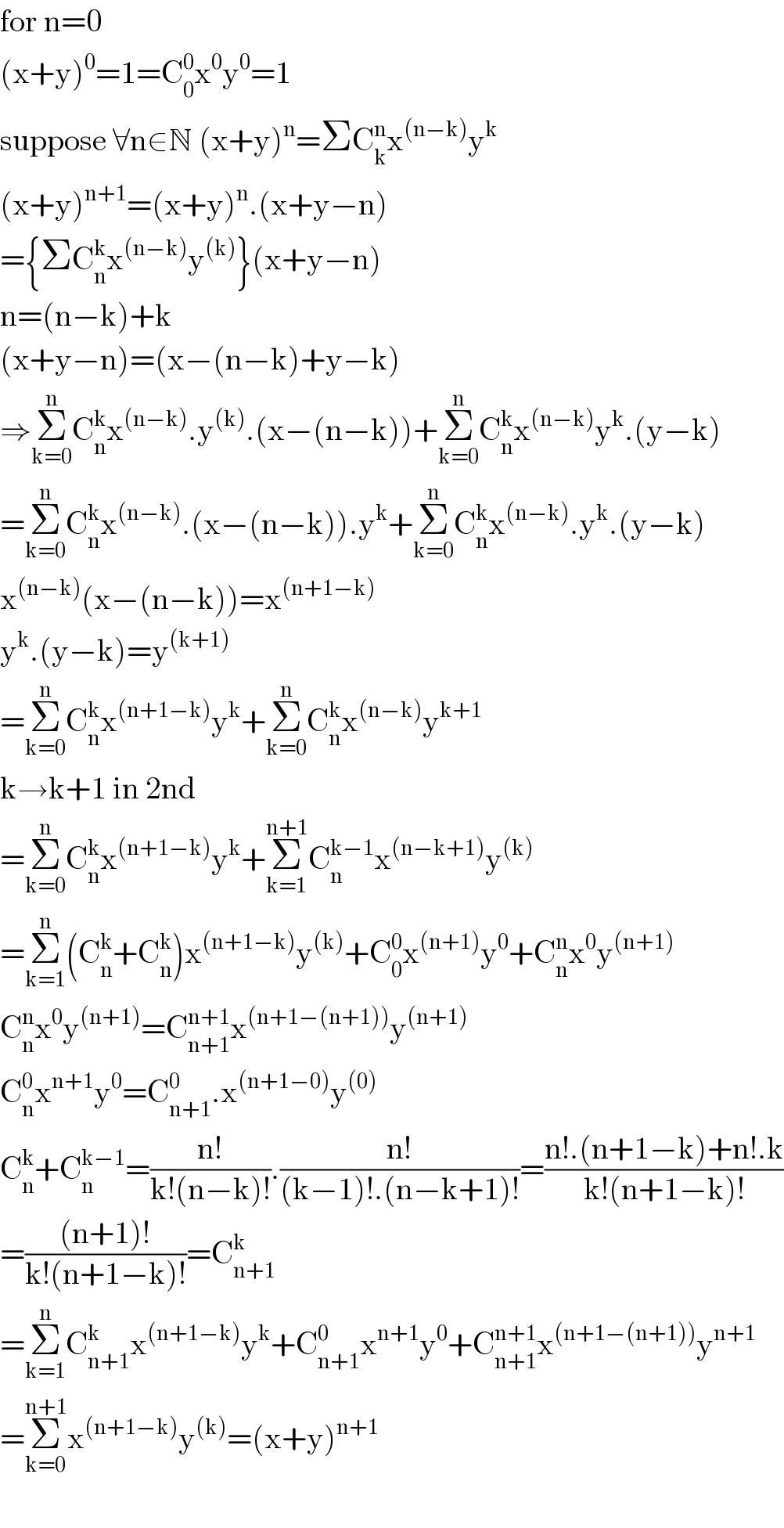
$$\mathrm{for}\:\mathrm{n}=\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{0}} =\mathrm{1}=\mathrm{C}_{\mathrm{0}} ^{\mathrm{0}} \mathrm{x}^{\mathrm{0}} \mathrm{y}^{\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{suppose}\:\forall\mathrm{n}\in\mathbb{N}\:\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{n}} =\Sigma\mathrm{C}_{\mathrm{k}} ^{\mathrm{n}} \mathrm{x}^{\left(\mathrm{n}−\mathrm{k}\right)} \mathrm{y}^{\mathrm{k}} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{n}+\mathrm{1}} =\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{n}} .\left(\mathrm{x}+\mathrm{y}−\mathrm{n}\right) \\ $$$$=\left\{\Sigma\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{x}^{\left(\mathrm{n}−\mathrm{k}\right)} \mathrm{y}^{\left(\mathrm{k}\right)} \right\}\left(\mathrm{x}+\mathrm{y}−\mathrm{n}\right) \\ $$$$\mathrm{n}=\left(\mathrm{n}−\mathrm{k}\right)+\mathrm{k} \\ $$$$\left(\mathrm{x}+\mathrm{y}−\mathrm{n}\right)=\left(\mathrm{x}−\left(\mathrm{n}−\mathrm{k}\right)+\mathrm{y}−\mathrm{k}\right) \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{x}^{\left(\mathrm{n}−\mathrm{k}\right)} .\mathrm{y}^{\left(\mathrm{k}\right)} .\left(\mathrm{x}−\left(\mathrm{n}−\mathrm{k}\right)\right)+\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{x}^{\left(\mathrm{n}−\mathrm{k}\right)} \mathrm{y}^{\mathrm{k}} .\left(\mathrm{y}−\mathrm{k}\right) \\ $$$$=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{x}^{\left(\mathrm{n}−\mathrm{k}\right)} .\left(\mathrm{x}−\left(\mathrm{n}−\mathrm{k}\right)\right).\mathrm{y}^{\mathrm{k}} +\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{x}^{\left(\mathrm{n}−\mathrm{k}\right)} .\mathrm{y}^{\mathrm{k}} .\left(\mathrm{y}−\mathrm{k}\right) \\ $$$$\mathrm{x}^{\left(\mathrm{n}−\mathrm{k}\right)} \left(\mathrm{x}−\left(\mathrm{n}−\mathrm{k}\right)\right)=\mathrm{x}^{\left(\mathrm{n}+\mathrm{1}−\mathrm{k}\right)} \\ $$$$\mathrm{y}^{\mathrm{k}} .\left(\mathrm{y}−\mathrm{k}\right)=\mathrm{y}^{\left(\mathrm{k}+\mathrm{1}\right)} \\ $$$$=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{x}^{\left(\mathrm{n}+\mathrm{1}−\mathrm{k}\right)} \mathrm{y}^{\mathrm{k}} +\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{x}^{\left(\mathrm{n}−\mathrm{k}\right)} \mathrm{y}^{\mathrm{k}+\mathrm{1}} \\ $$$$\mathrm{k}\rightarrow\mathrm{k}+\mathrm{1}\:\mathrm{in}\:\mathrm{2nd}\: \\ $$$$=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{x}^{\left(\mathrm{n}+\mathrm{1}−\mathrm{k}\right)} \mathrm{y}^{\mathrm{k}} +\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}+\mathrm{1}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}−\mathrm{1}} \mathrm{x}^{\left(\mathrm{n}−\mathrm{k}+\mathrm{1}\right)} \mathrm{y}^{\left(\mathrm{k}\right)} \\ $$$$=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} +\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \right)\mathrm{x}^{\left(\mathrm{n}+\mathrm{1}−\mathrm{k}\right)} \mathrm{y}^{\left(\mathrm{k}\right)} +\mathrm{C}_{\mathrm{0}} ^{\mathrm{0}} \mathrm{x}^{\left(\mathrm{n}+\mathrm{1}\right)} \mathrm{y}^{\mathrm{0}} +\mathrm{C}_{\mathrm{n}} ^{\mathrm{n}} \mathrm{x}^{\mathrm{0}} \mathrm{y}^{\left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$\mathrm{C}_{\mathrm{n}} ^{\mathrm{n}} \mathrm{x}^{\mathrm{0}} \mathrm{y}^{\left(\mathrm{n}+\mathrm{1}\right)} =\mathrm{C}_{\mathrm{n}+\mathrm{1}} ^{\mathrm{n}+\mathrm{1}} \mathrm{x}^{\left(\mathrm{n}+\mathrm{1}−\left(\mathrm{n}+\mathrm{1}\right)\right)} \mathrm{y}^{\left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$\mathrm{C}_{\mathrm{n}} ^{\mathrm{0}} \mathrm{x}^{\mathrm{n}+\mathrm{1}} \mathrm{y}^{\mathrm{0}} =\mathrm{C}_{\mathrm{n}+\mathrm{1}} ^{\mathrm{0}} .\mathrm{x}^{\left(\mathrm{n}+\mathrm{1}−\mathrm{0}\right)} \mathrm{y}^{\left(\mathrm{0}\right)} \\ $$$$\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} +\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}−\mathrm{1}} =\frac{\mathrm{n}!}{\mathrm{k}!\left(\mathrm{n}−\mathrm{k}\right)!}.\frac{\mathrm{n}!}{\left(\mathrm{k}−\mathrm{1}\right)!.\left(\mathrm{n}−\mathrm{k}+\mathrm{1}\right)!}=\frac{\mathrm{n}!.\left(\mathrm{n}+\mathrm{1}−\mathrm{k}\right)+\mathrm{n}!.\mathrm{k}}{\mathrm{k}!\left(\mathrm{n}+\mathrm{1}−\mathrm{k}\right)!} \\ $$$$=\frac{\left(\mathrm{n}+\mathrm{1}\right)!}{\mathrm{k}!\left(\mathrm{n}+\mathrm{1}−\mathrm{k}\right)!}=\mathrm{C}_{\mathrm{n}+\mathrm{1}} ^{\mathrm{k}} \\ $$$$=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}+\mathrm{1}} ^{\mathrm{k}} \mathrm{x}^{\left(\mathrm{n}+\mathrm{1}−\mathrm{k}\right)} \mathrm{y}^{\mathrm{k}} +\mathrm{C}_{\mathrm{n}+\mathrm{1}} ^{\mathrm{0}} \mathrm{x}^{\mathrm{n}+\mathrm{1}} \mathrm{y}^{\mathrm{0}} +\mathrm{C}_{\mathrm{n}+\mathrm{1}} ^{\mathrm{n}+\mathrm{1}} \mathrm{x}^{\left(\mathrm{n}+\mathrm{1}−\left(\mathrm{n}+\mathrm{1}\right)\right)} \mathrm{y}^{\mathrm{n}+\mathrm{1}} \\ $$$$=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}+\mathrm{1}} {\sum}}\mathrm{x}^{\left(\mathrm{n}+\mathrm{1}−\mathrm{k}\right)} \mathrm{y}^{\left(\mathrm{k}\right)} =\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{n}+\mathrm{1}} \: \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 05/Nov/19

$${thank}\:{you}\:{sir}. \\ $$
Commented by mind is power last updated on 06/Nov/19

$$\mathrm{most}\:\mathrm{welcom} \\ $$
