Question Number 1034 by 123456 last updated on 21/May/15
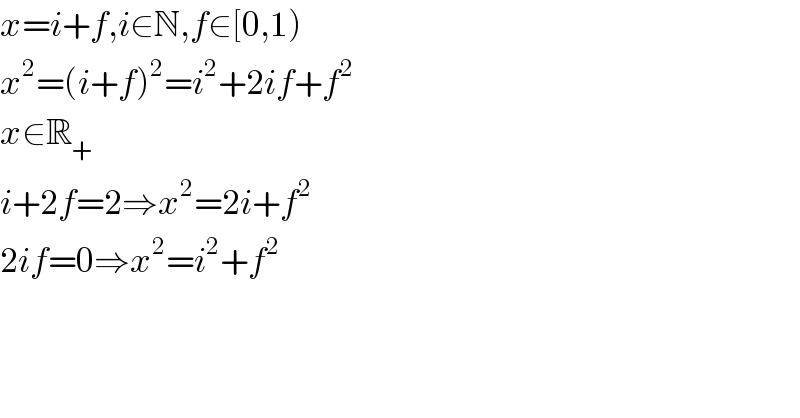
$${x}={i}+{f},{i}\in\mathbb{N},{f}\in\left[\mathrm{0},\mathrm{1}\right) \\ $$$${x}^{\mathrm{2}} =\left({i}+{f}\right)^{\mathrm{2}} ={i}^{\mathrm{2}} +\mathrm{2}{if}+{f}^{\mathrm{2}} \\ $$$${x}\in\mathbb{R}_{+} \\ $$$${i}+\mathrm{2}{f}=\mathrm{2}\Rightarrow{x}^{\mathrm{2}} =\mathrm{2}{i}+{f}^{\mathrm{2}} \\ $$$$\mathrm{2}{if}=\mathrm{0}\Rightarrow{x}^{\mathrm{2}} ={i}^{\mathrm{2}} +{f}^{\mathrm{2}} \\ $$
Answered by prakash jain last updated on 21/May/15

$$\mathrm{2}{if}=\mathrm{0}\Rightarrow{i}=\mathrm{0}\vee{f}=\mathrm{0} \\ $$$$\because{f}<\mathrm{1},\:{i}+\mathrm{2}{f}=\mathrm{2}\:\:\Rightarrow{i}>\mathrm{0} \\ $$$${f}=\mathrm{0},{i}=\mathrm{2} \\ $$$${x}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} \Rightarrow{x}=\pm\mathrm{2} \\ $$
