Question Number 11648 by uni last updated on 29/Mar/17

$$\mid\mathrm{x}\mid<\mathrm{l} \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{x}^{\mathrm{n}} =? \\ $$
Answered by Nayon last updated on 29/Mar/17
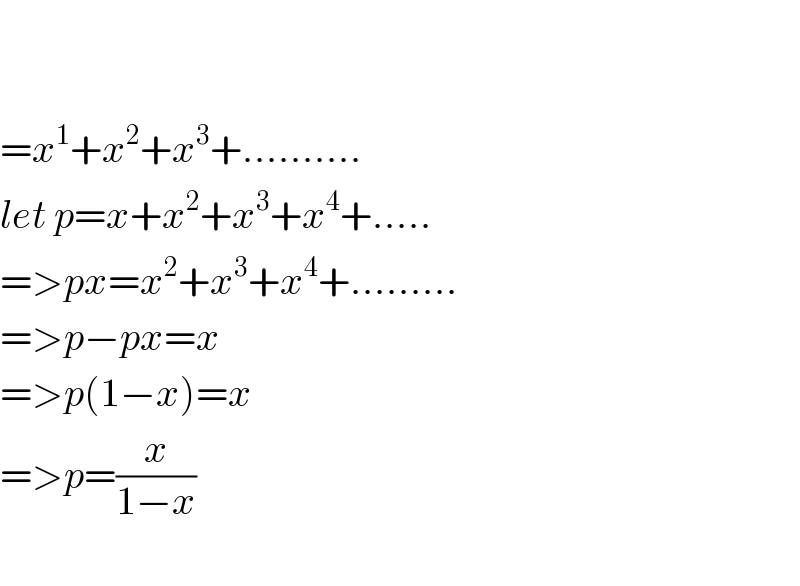
$$ \\ $$$$ \\ $$$$={x}^{\mathrm{1}} +{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +………. \\ $$$${let}\:{p}={x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +….. \\ $$$$=>{px}={x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +……… \\ $$$$=>{p}−{px}={x} \\ $$$$=>{p}\left(\mathrm{1}−{x}\right)={x} \\ $$$$=>{p}=\frac{{x}}{\mathrm{1}−{x}}\: \\ $$$$ \\ $$
