Question Number 143628 by ArielVyny last updated on 16/Jun/21

$$\int_{{x}} ^{\propto} {t}^{\alpha−\mathrm{1}} {e}^{{it}} {dt}=?? \\ $$
Answered by mathmax by abdo last updated on 16/Jun/21
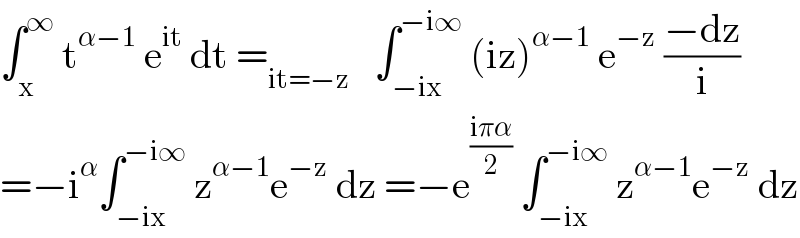
$$\int_{\mathrm{x}} ^{\infty} \:\mathrm{t}^{\alpha−\mathrm{1}} \:\mathrm{e}^{\mathrm{it}} \:\mathrm{dt}\:=_{\mathrm{it}=−\mathrm{z}} \:\:\:\int_{−\mathrm{ix}} ^{−\mathrm{i}\infty} \:\left(\mathrm{iz}\right)^{\alpha−\mathrm{1}} \:\mathrm{e}^{−\mathrm{z}} \:\frac{−\mathrm{dz}}{\mathrm{i}} \\ $$$$=−\mathrm{i}^{\alpha} \int_{−\mathrm{ix}} ^{−\mathrm{i}\infty} \:\mathrm{z}^{\alpha−\mathrm{1}} \mathrm{e}^{−\mathrm{z}} \:\mathrm{dz}\:=−\mathrm{e}^{\frac{\mathrm{i}\pi\alpha}{\mathrm{2}}} \:\int_{−\mathrm{ix}} ^{−\mathrm{i}\infty} \:\mathrm{z}^{\alpha−\mathrm{1}} \mathrm{e}^{−\mathrm{z}} \:\mathrm{dz} \\ $$
