x-x-1-2-dx-y-2y-1-2-dy-1-4sec-x-dx-y-sec-3-2x-5-y-

Question Number 5048 by LMTV last updated on 05/Apr/16

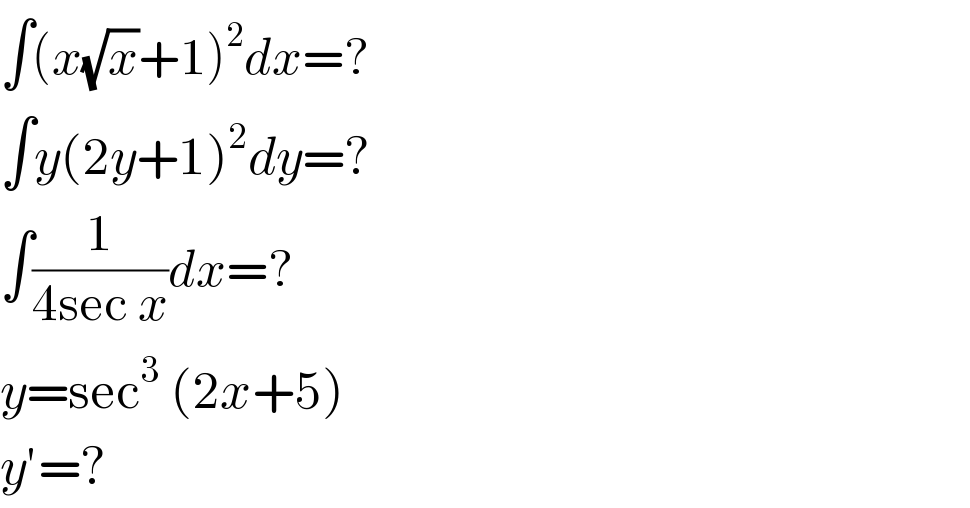
$$\int\left({x}\sqrt{{x}}+\mathrm{1}\right)^{\mathrm{2}} {dx}=? \\ $$$$\int{y}\left(\mathrm{2}{y}+\mathrm{1}\right)^{\mathrm{2}} {dy}=? \\ $$$$\int\frac{\mathrm{1}}{\mathrm{4sec}\:{x}}{dx}=? \\ $$$${y}=\mathrm{sec}^{\mathrm{3}} \:\left(\mathrm{2}{x}+\mathrm{5}\right) \\ $$$${y}'=? \\ $$

Commented by prakash jain last updated on 05/Apr/16

$${y}=\mathrm{sec}^{\mathrm{3}} \left(\mathrm{2}{x}+\mathrm{5}\right) \\ $$$$\mathrm{Successive}\:\mathrm{application}\:\mathrm{of}\:\mathrm{Chain}\:\mathrm{rule}\:\frac{{dy}}{{dx}}=\frac{{dy}}{{du}}\centerdot\frac{{du}}{{dx}} \\ $$$${y}'=\mathrm{3sec}^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{5}\right)\left[\mathrm{sec}\:\left(\mathrm{2}{x}+\mathrm{5}\right)\mathrm{tan}\:\left(\mathrm{2}{x}+\mathrm{5}\right)\right]\left[\mathrm{2}\right] \\ $$$$=\mathrm{6sec}^{\mathrm{3}} \left(\mathrm{2}{x}+\mathrm{5}\right)\mathrm{tan}\:\left(\mathrm{2}{x}+\mathrm{5}\right) \\ $$$$\int\frac{\mathrm{1}}{\mathrm{4sec}\:{x}}\mathrm{d}{x}=\frac{\mathrm{1}}{\mathrm{4}}\int\mathrm{cos}\:{x}\:\mathrm{d}{x}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:{x}+{C} \\ $$

Answered by prakash jain last updated on 05/Apr/16

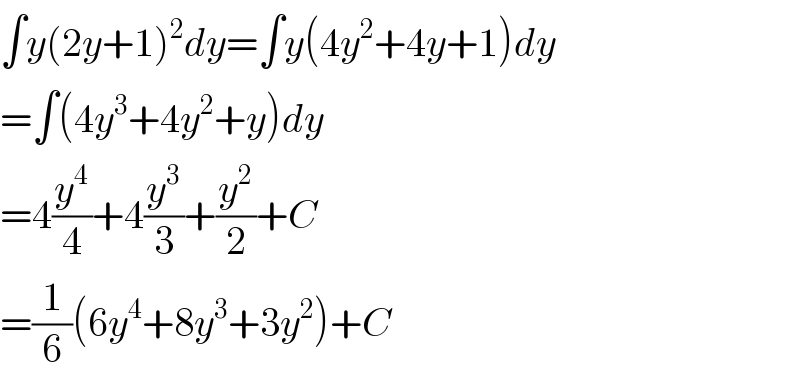
$$\int{y}\left(\mathrm{2}{y}+\mathrm{1}\right)^{\mathrm{2}} {dy}=\int{y}\left(\mathrm{4}{y}^{\mathrm{2}} +\mathrm{4}{y}+\mathrm{1}\right){dy} \\ $$$$=\int\left(\mathrm{4}{y}^{\mathrm{3}} +\mathrm{4}{y}^{\mathrm{2}} +{y}\right){dy} \\ $$$$=\mathrm{4}\frac{{y}^{\mathrm{4}} }{\mathrm{4}}+\mathrm{4}\frac{{y}^{\mathrm{3}} }{\mathrm{3}}+\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{6}{y}^{\mathrm{4}} +\mathrm{8}{y}^{\mathrm{3}} +\mathrm{3}{y}^{\mathrm{2}} \right)+{C} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com