Menu Close

x-x-2-1-y-y-4-4-9-x-y-4-4-y-x-2-1-

Tinku Tara 0 Comments
Pin




Question Number 137594 by Ñï= last updated on 04/Apr/21
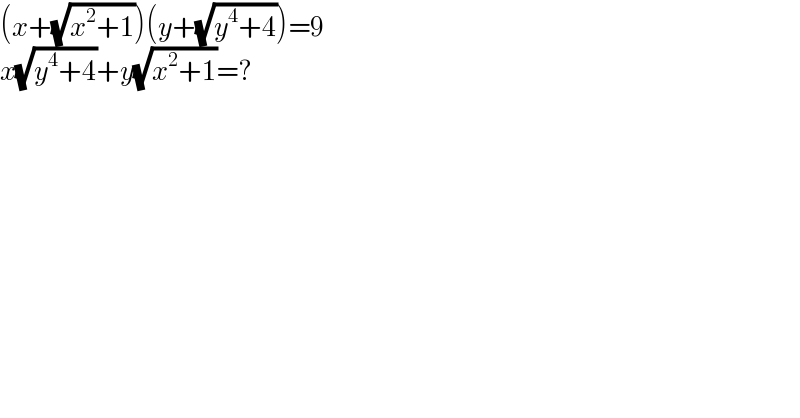
(x+(√(x^2 +1)))(y+(√(y^4 +4)))=9 x(√(y^4 +4))+y(√(x^2 +1))=?
$$\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\left({y}+\sqrt{{y}^{\mathrm{4}} +\mathrm{4}}\right)=\mathrm{9} \\ $$$${x}\sqrt{{y}^{\mathrm{4}} +\mathrm{4}}+{y}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}=? \\ $$
Answered by bemath last updated on 04/Apr/21
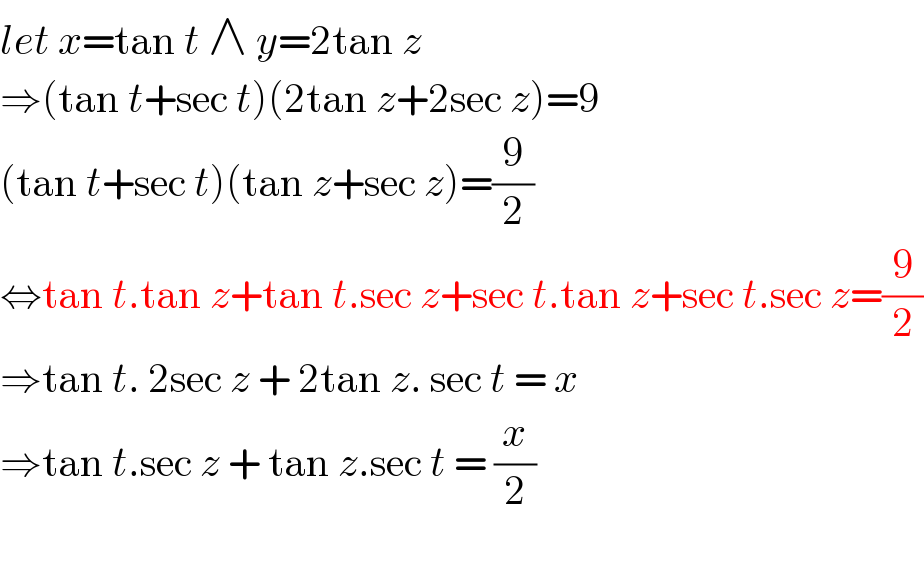
let x=tan t ∧ y=2tan z ⇒(tan t+sec t)(2tan z+2sec z)=9 (tan t+sec t)(tan z+sec z)=(9/2) ⇔tan t.tan z+tan t.sec z+sec t.tan z+sec t.sec z=(9/2) ⇒tan t. 2sec z + 2tan z. sec t = x ⇒tan t.sec z + tan z.sec t = (x/2)
$${let}\:{x}=\mathrm{tan}\:{t}\:\wedge\:{y}=\mathrm{2tan}\:{z} \\ $$$$\Rightarrow\left(\mathrm{tan}\:{t}+\mathrm{sec}\:{t}\right)\left(\mathrm{2tan}\:{z}+\mathrm{2sec}\:{z}\right)=\mathrm{9} \\ $$$$\left(\mathrm{tan}\:{t}+\mathrm{sec}\:{t}\right)\left(\mathrm{tan}\:{z}+\mathrm{sec}\:{z}\right)=\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{tan}\:{t}.\mathrm{tan}\:{z}+\mathrm{tan}\:{t}.\mathrm{sec}\:{z}+\mathrm{sec}\:{t}.\mathrm{tan}\:{z}+\mathrm{sec}\:{t}.\mathrm{sec}\:{z}=\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:{t}.\:\mathrm{2sec}\:{z}\:+\:\mathrm{2tan}\:{z}.\:\mathrm{sec}\:{t}\:=\:{x} \\ $$$$\Rightarrow\mathrm{tan}\:{t}.\mathrm{sec}\:{z}\:+\:\mathrm{tan}\:{z}.\mathrm{sec}\:{t}\:=\:\frac{{x}}{\mathrm{2}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *