Menu Close

x-x-3-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 6107 by gourav~ last updated on 14/Jun/16
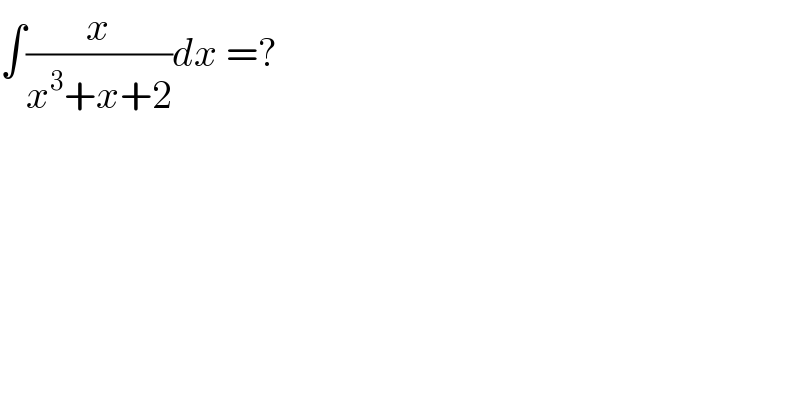
∫(x/(x^3 +x+2))dx =?
$$\int\frac{{x}}{{x}^{\mathrm{3}} +{x}+\mathrm{2}}{dx}\:=? \\ $$
Commented by Yozzii last updated on 14/Jun/16
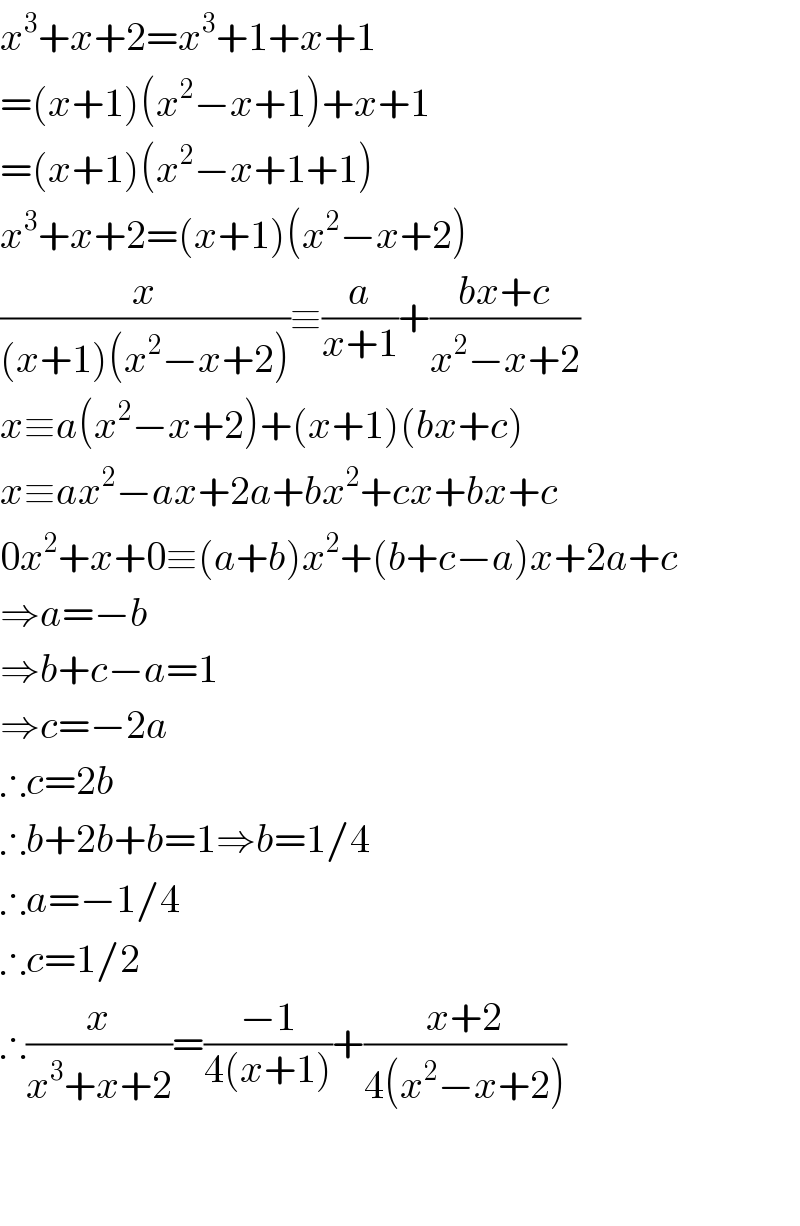
x^3 +x+2=x^3 +1+x+1 =(x+1)(x^2 −x+1)+x+1 =(x+1)(x^2 −x+1+1) x^3 +x+2=(x+1)(x^2 −x+2) (x/((x+1)(x^2 −x+2)))≡(a/(x+1))+((bx+c)/(x^2 −x+2)) x≡a(x^2 −x+2)+(x+1)(bx+c) x≡ax^2 −ax+2a+bx^2 +cx+bx+c 0x^2 +x+0≡(a+b)x^2 +(b+c−a)x+2a+c ⇒a=−b ⇒b+c−a=1 ⇒c=−2a ∴c=2b ∴b+2b+b=1⇒b=1/4 ∴a=−1/4 ∴c=1/2 ∴(x/(x^3 +x+2))=((−1)/(4(x+1)))+((x+2)/(4(x^2 −x+2)))
$${x}^{\mathrm{3}} +{x}+\mathrm{2}={x}^{\mathrm{3}} +\mathrm{1}+{x}+\mathrm{1} \\ $$$$=\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)+{x}+\mathrm{1} \\ $$$$=\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}+\mathrm{1}\right) \\ $$$${x}^{\mathrm{3}} +{x}+\mathrm{2}=\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right) \\ $$$$\frac{{x}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)}\equiv\frac{{a}}{{x}+\mathrm{1}}+\frac{{bx}+{c}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}} \\ $$$${x}\equiv{a}\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)+\left({x}+\mathrm{1}\right)\left({bx}+{c}\right) \\ $$$${x}\equiv{ax}^{\mathrm{2}} −{ax}+\mathrm{2}{a}+{bx}^{\mathrm{2}} +{cx}+{bx}+{c} \\ $$$$\mathrm{0}{x}^{\mathrm{2}} +{x}+\mathrm{0}\equiv\left({a}+{b}\right){x}^{\mathrm{2}} +\left({b}+{c}−{a}\right){x}+\mathrm{2}{a}+{c} \\ $$$$\Rightarrow{a}=−{b} \\ $$$$\Rightarrow{b}+{c}−{a}=\mathrm{1} \\ $$$$\Rightarrow{c}=−\mathrm{2}{a} \\ $$$$\therefore{c}=\mathrm{2}{b} \\ $$$$\therefore{b}+\mathrm{2}{b}+{b}=\mathrm{1}\Rightarrow{b}=\mathrm{1}/\mathrm{4} \\ $$$$\therefore{a}=−\mathrm{1}/\mathrm{4} \\ $$$$\therefore{c}=\mathrm{1}/\mathrm{2} \\ $$$$\therefore\frac{{x}}{{x}^{\mathrm{3}} +{x}+\mathrm{2}}=\frac{−\mathrm{1}}{\mathrm{4}\left({x}+\mathrm{1}\right)}+\frac{{x}+\mathrm{2}}{\mathrm{4}\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)} \\ $$$$ \\ $$$$ \\ $$
Answered by Yozzii last updated on 14/Jun/16
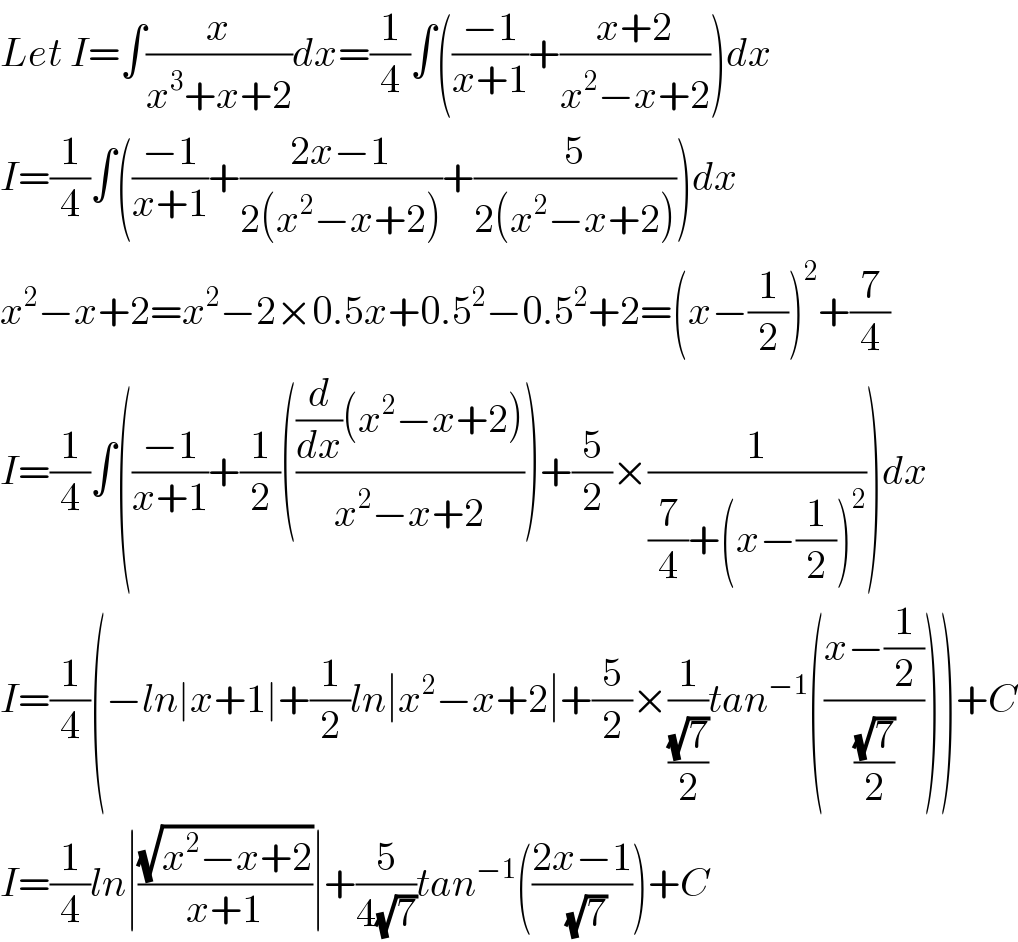
Let I=∫(x/(x^3 +x+2))dx=(1/4)∫(((−1)/(x+1))+((x+2)/(x^2 −x+2)))dx I=(1/4)∫(((−1)/(x+1))+((2x−1)/(2(x^2 −x+2)))+(5/(2(x^2 −x+2))))dx x^2 −x+2=x^2 −2×0.5x+0.5^2 −0.5^2 +2=(x−(1/2))^2 +(7/4) I=(1/4)∫(((−1)/(x+1))+(1/2)((((d/dx)(x^2 −x+2))/(x^2 −x+2)))+(5/2)×(1/((7/4)+(x−(1/2))^2 )))dx I=(1/4)(−ln∣x+1∣+(1/2)ln∣x^2 −x+2∣+(5/2)×(1/((√7)/2))tan^(−1) (((x−(1/2))/((√7)/2))))+C I=(1/4)ln∣((√(x^2 −x+2))/(x+1))∣+(5/(4(√7)))tan^(−1) (((2x−1)/( (√7))))+C
$${Let}\:{I}=\int\frac{{x}}{{x}^{\mathrm{3}} +{x}+\mathrm{2}}{dx}=\frac{\mathrm{1}}{\mathrm{4}}\int\left(\frac{−\mathrm{1}}{{x}+\mathrm{1}}+\frac{{x}+\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}}\right){dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{4}}\int\left(\frac{−\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)}+\frac{\mathrm{5}}{\mathrm{2}\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)}\right){dx} \\ $$$${x}^{\mathrm{2}} −{x}+\mathrm{2}={x}^{\mathrm{2}} −\mathrm{2}×\mathrm{0}.\mathrm{5}{x}+\mathrm{0}.\mathrm{5}^{\mathrm{2}} −\mathrm{0}.\mathrm{5}^{\mathrm{2}} +\mathrm{2}=\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{7}}{\mathrm{4}} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{4}}\int\left(\frac{−\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\frac{{d}}{{dx}}\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)}{{x}^{\mathrm{2}} −{x}+\mathrm{2}}\right)+\frac{\mathrm{5}}{\mathrm{2}}×\frac{\mathrm{1}}{\frac{\mathrm{7}}{\mathrm{4}}+\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\right){dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{4}}\left(−{ln}\mid{x}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} −{x}+\mathrm{2}\mid+\frac{\mathrm{5}}{\mathrm{2}}×\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}}\right)\right)+{C} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\frac{\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{2}}}{{x}+\mathrm{1}}\mid+\frac{\mathrm{5}}{\mathrm{4}\sqrt{\mathrm{7}}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{7}}}\right)+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *