Question Number 142415 by Rankut last updated on 31/May/21
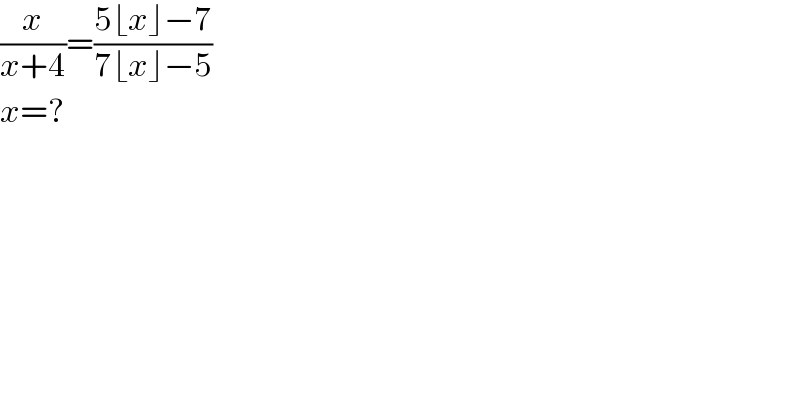
$$\frac{{x}}{{x}+\mathrm{4}}=\frac{\mathrm{5}\lfloor{x}\rfloor−\mathrm{7}}{\mathrm{7}\lfloor{x}\rfloor−\mathrm{5}} \\ $$$${x}=? \\ $$
Answered by mr W last updated on 31/May/21

$${say}\:{x}={n}+{f} \\ $$$$\frac{{n}+{f}}{{n}+{f}+\mathrm{4}}=\frac{\mathrm{5}{n}−\mathrm{7}}{\mathrm{7}{n}−\mathrm{5}} \\ $$$$\mathrm{7}{n}^{\mathrm{2}} +\mathrm{7}{fn}−\mathrm{5}{n}−\mathrm{5}{f}=\mathrm{5}{n}^{\mathrm{2}} +\mathrm{5}\left({f}+\mathrm{4}\right){n}−\mathrm{7}{n}−\mathrm{7}\left({f}+\mathrm{4}\right) \\ $$$${f}=\frac{\mathrm{9}{n}−{n}^{\mathrm{2}} −\mathrm{14}}{{n}+\mathrm{1}}\geqslant\mathrm{0} \\ $$$${n}^{\mathrm{2}} −\mathrm{9}{n}+\mathrm{14}\leqslant\mathrm{0} \\ $$$$\left({n}−\mathrm{2}\right)\left({n}−\mathrm{7}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\leqslant{n}\leqslant\mathrm{7} \\ $$$${f}=\frac{\mathrm{9}{n}−{n}^{\mathrm{2}} −\mathrm{14}}{{n}+\mathrm{1}}<\mathrm{1} \\ $$$${n}^{\mathrm{2}} −\mathrm{8}{n}+\mathrm{15}>\mathrm{0} \\ $$$$\left({n}−\mathrm{3}\right)\left({n}−\mathrm{5}\right)>\mathrm{0} \\ $$$$\Rightarrow{n}<\mathrm{3}\:{or}\:{n}>\mathrm{5} \\ $$$$\Rightarrow{n}=\mathrm{2},\:\mathrm{6},\:\mathrm{7} \\ $$$$ \\ $$$${f}=\frac{\mathrm{9}×\mathrm{2}−\mathrm{2}^{\mathrm{2}} −\mathrm{14}}{\mathrm{2}+\mathrm{1}}=\mathrm{0}\:\Rightarrow{x}=\mathrm{2} \\ $$$${f}=\frac{\mathrm{9}×\mathrm{6}−\mathrm{6}^{\mathrm{2}} −\mathrm{14}}{\mathrm{6}+\mathrm{1}}=\frac{\mathrm{4}}{\mathrm{7}}\:\Rightarrow{x}=\mathrm{6}\frac{\mathrm{4}}{\mathrm{7}} \\ $$$${f}=\frac{\mathrm{9}×\mathrm{7}−\mathrm{7}^{\mathrm{2}} −\mathrm{14}}{\mathrm{7}+\mathrm{1}}=\mathrm{0}\:\Rightarrow{x}=\mathrm{7} \\ $$
