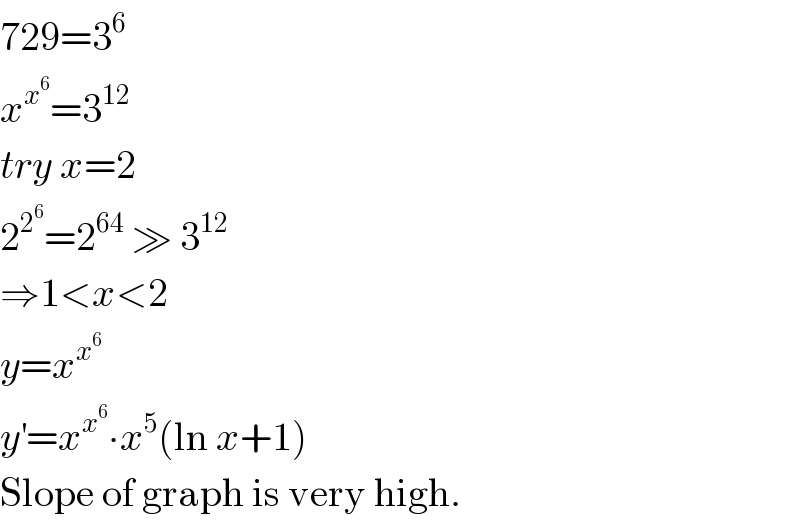x-x-6-729-find-x-

Question Number 6523 by Tawakalitu. last updated on 30/Jun/16

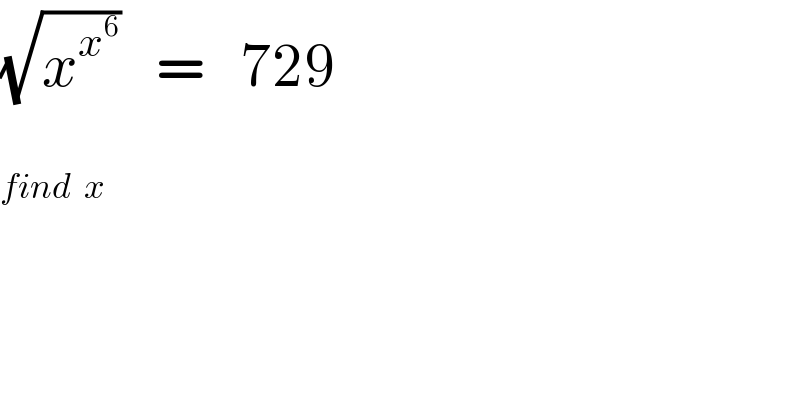
\sqrt{x^{x^{6}}} = 729

f i n d x

Commented by Rasheed Soomro last updated on 01/Jul/16

\sqrt{x^{x^{6}}} = 729

I f x i s a w h o l e n u m b e r

x^{\frac{1}{2} x^{6}} = {(x^{1 / 2})}^{x^{6}} = 729

A s l h s i s w h o l e n u m b e r

S o x i s p e r f e c t s q u a r e OR 2 ∣ x^{6} i - e x i s e v e n

B u t i f x w e r e e v e n x^{x^{6}} w e r e a l s o e v e n b u t

x^{x^{6}} i s o d d a n d e q u a l t o 729^{2}

H e n c e x i s a n o d d p e r f e c t s q u a r e .

C o n t i n u e

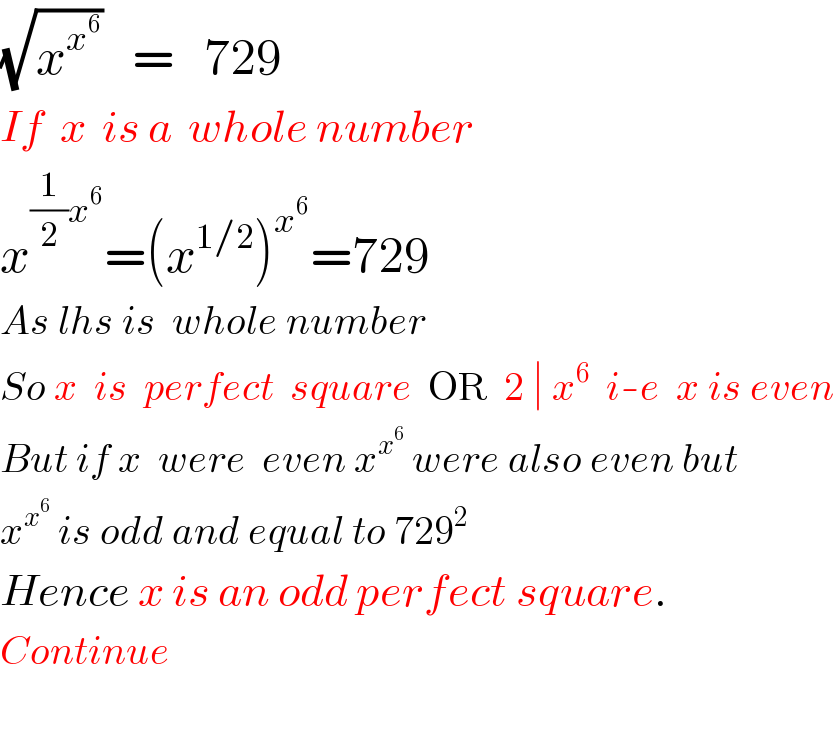
Commented by Temp last updated on 01/Jul/16

D o o d d s q u a r e s e x i s t ?

Commented by Rasheed Soomro last updated on 01/Jul/16

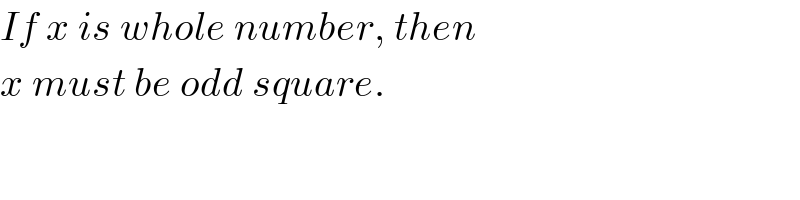
I f x i s w h o l e n u m b e r, t h e n

x m u s t b e o d d s q u a r e .

Commented by prakash jain last updated on 01/Jul/16

729 = 3^{6}

x^{x^{6}} = 3^{12}

t r y x = 2

2^{2^{6}} = 2^{64} ≫ 3^{12}

\Rightarrow 1 < x < 2

y = x^{x^{6}}

y^{^{'}} = x^{x^{6}} \cdot x^{5} (\ln x + 1)

Slope of graph is very high .