Question Number 131697 by mathlove last updated on 07/Feb/21

$${x}^{{x}} =\mathrm{6}\:\:\:\:\:\:\:\:\:\:{x}=? \\ $$
Answered by mr W last updated on 07/Feb/21
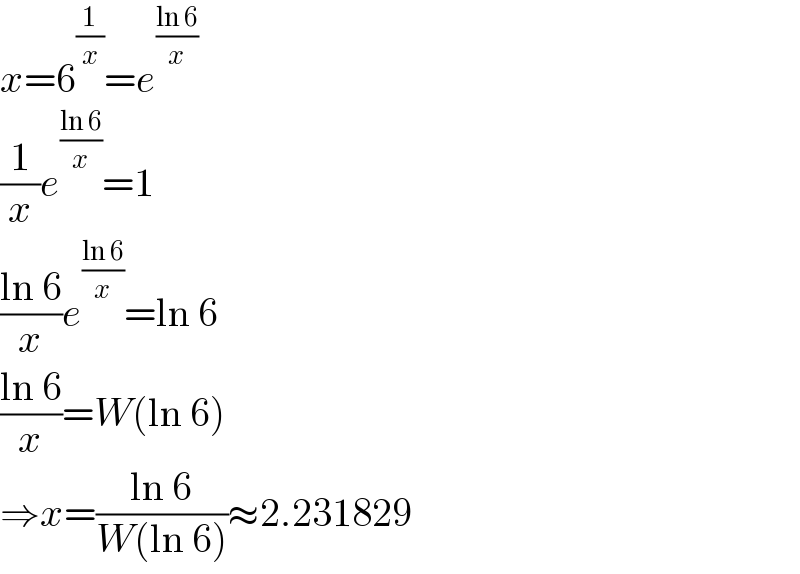
$${x}=\mathrm{6}^{\frac{\mathrm{1}}{{x}}} ={e}^{\frac{\mathrm{ln}\:\mathrm{6}}{{x}}} \\ $$$$\frac{\mathrm{1}}{{x}}{e}^{\frac{\mathrm{ln}\:\mathrm{6}}{{x}}} =\mathrm{1} \\ $$$$\frac{\mathrm{ln}\:\mathrm{6}}{{x}}{e}^{\frac{\mathrm{ln}\:\mathrm{6}}{{x}}} =\mathrm{ln}\:\mathrm{6} \\ $$$$\frac{\mathrm{ln}\:\mathrm{6}}{{x}}={W}\left(\mathrm{ln}\:\mathrm{6}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{ln}\:\mathrm{6}}{{W}\left(\mathrm{ln}\:\mathrm{6}\right)}\approx\mathrm{2}.\mathrm{231829} \\ $$
Commented by mathlove last updated on 07/Feb/21

$${thanks}\:{sir} \\ $$
Commented by mathlove last updated on 07/Feb/21

$${what}\:\:{W}\left({ln}\mathrm{6}\right)=? \\ $$
Commented by mr W last updated on 07/Feb/21

$${Lambert}\:{W}\:{function} \\ $$$${W}\left(\mathrm{ln}\:\mathrm{6}\right)\approx\mathrm{0}.\mathrm{802821260392} \\ $$
Answered by Dwaipayan Shikari last updated on 07/Feb/21

$${x}^{{x}} =\mathrm{6} \\ $$$$\Rightarrow{xlog}\left({x}\right)={log}\left(\mathrm{6}\right)\Rightarrow{log}\left({x}\right){e}^{{log}\left({x}\right)} ={log}\left(\mathrm{6}\right)\Rightarrow{log}\left({x}\right)={W}_{\mathrm{0}} \left({log}\left(\mathrm{6}\right)\right) \\ $$$${x}={e}^{{W}_{\mathrm{0}} \left({log}\left(\mathrm{6}\right)\right)} =\frac{{log}\left(\mathrm{6}\right)}{{W}_{\mathrm{0}} \left({log}\left(\mathrm{6}\right)\right)} \\ $$$${x}=\frac{{log}\left(\mathrm{6}\right)}{{log}\left(\mathrm{6}\right)−{log}^{\mathrm{2}} \left(\mathrm{6}\right)+\frac{\mathrm{3}}{\mathrm{2}}{log}^{\mathrm{3}} \left(\mathrm{6}\right)−\frac{\mathrm{8}}{\mathrm{3}}{log}^{\mathrm{4}} \left(\mathrm{6}\right)+\frac{\mathrm{125}}{\mathrm{24}}{log}^{\mathrm{5}} \left(\mathrm{6}\right)−..} \\ $$$${Exact}\:{solution}\:{for}\:{x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{log}\left(\mathrm{6}\right)+\frac{\mathrm{3}}{\mathrm{2}}{log}^{\mathrm{2}} \left(\mathrm{6}\right)−\frac{\mathrm{8}}{\mathrm{3}}{log}^{\mathrm{3}} \left(\mathrm{6}\right)+…} \\ $$
Commented by I want to learn more last updated on 07/Feb/21
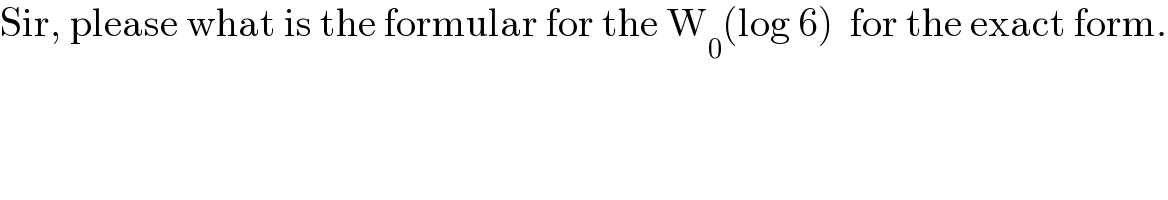
$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{formular}\:\mathrm{for}\:\mathrm{the}\:\mathrm{W}_{\mathrm{0}} \left(\mathrm{log}\:\mathrm{6}\right)\:\:\mathrm{for}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{form}. \\ $$
Commented by Dwaipayan Shikari last updated on 07/Feb/21

$${Asymtotic}\:{relation} \\ $$$${W}_{\mathrm{0}} \left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}{x}^{{n}} \\ $$
Commented by I want to learn more last updated on 07/Feb/21
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}. \\ $$
