Question Number 139799 by Study last updated on 01/May/21
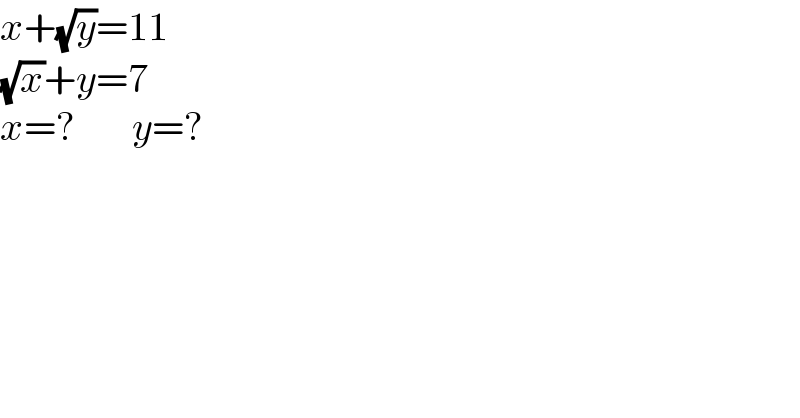
$${x}+\sqrt{{y}}=\mathrm{11} \\ $$$$\sqrt{{x}}+{y}=\mathrm{7} \\ $$$${x}=?\:\:\:\:\:\:\:{y}=? \\ $$
Commented by MJS_new last updated on 01/May/21
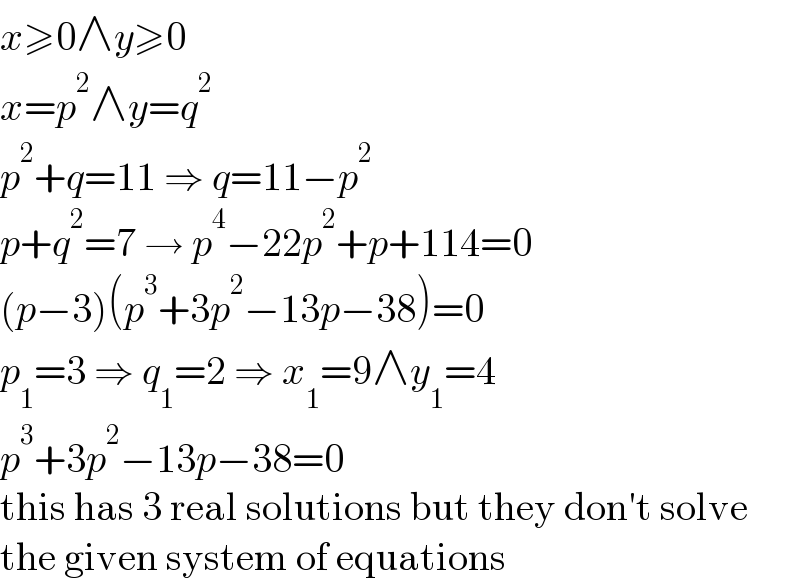
$${x}\geqslant\mathrm{0}\wedge{y}\geqslant\mathrm{0} \\ $$$${x}={p}^{\mathrm{2}} \wedge{y}={q}^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} +{q}=\mathrm{11}\:\Rightarrow\:{q}=\mathrm{11}−{p}^{\mathrm{2}} \\ $$$${p}+{q}^{\mathrm{2}} =\mathrm{7}\:\rightarrow\:{p}^{\mathrm{4}} −\mathrm{22}{p}^{\mathrm{2}} +{p}+\mathrm{114}=\mathrm{0} \\ $$$$\left({p}−\mathrm{3}\right)\left({p}^{\mathrm{3}} +\mathrm{3}{p}^{\mathrm{2}} −\mathrm{13}{p}−\mathrm{38}\right)=\mathrm{0} \\ $$$${p}_{\mathrm{1}} =\mathrm{3}\:\Rightarrow\:{q}_{\mathrm{1}} =\mathrm{2}\:\Rightarrow\:{x}_{\mathrm{1}} =\mathrm{9}\wedge{y}_{\mathrm{1}} =\mathrm{4} \\ $$$${p}^{\mathrm{3}} +\mathrm{3}{p}^{\mathrm{2}} −\mathrm{13}{p}−\mathrm{38}=\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{3}\:\mathrm{real}\:\mathrm{solutions}\:\mathrm{but}\:\mathrm{they}\:\mathrm{don}'\mathrm{t}\:\mathrm{solve} \\ $$$$\mathrm{the}\:\mathrm{given}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations} \\ $$
Answered by bramlexs22 last updated on 01/May/21

$$\begin{cases}{\mathrm{x}=\mathrm{9}}\\{\mathrm{y}=\mathrm{4}}\end{cases} \\ $$
Commented by Study last updated on 01/May/21
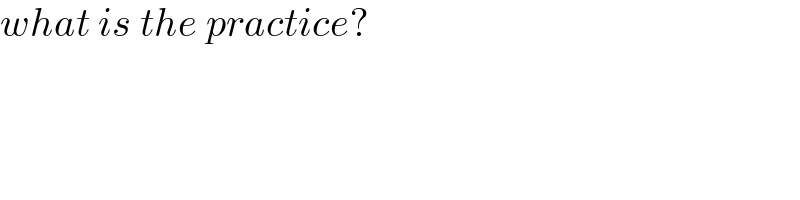
$${what}\:{is}\:{the}\:{practice}? \\ $$
