Question Number 10012 by konen last updated on 20/Jan/17
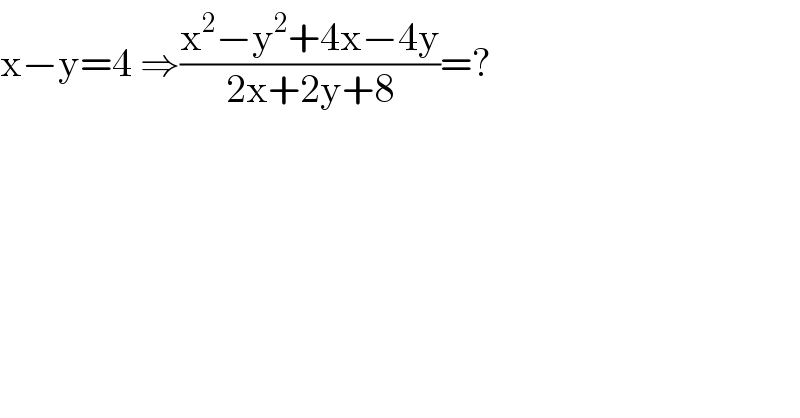
$$\mathrm{x}−\mathrm{y}=\mathrm{4}\:\Rightarrow\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{4x}−\mathrm{4y}}{\mathrm{2x}+\mathrm{2y}+\mathrm{8}}=? \\ $$
Answered by nume1114 last updated on 21/Jan/17
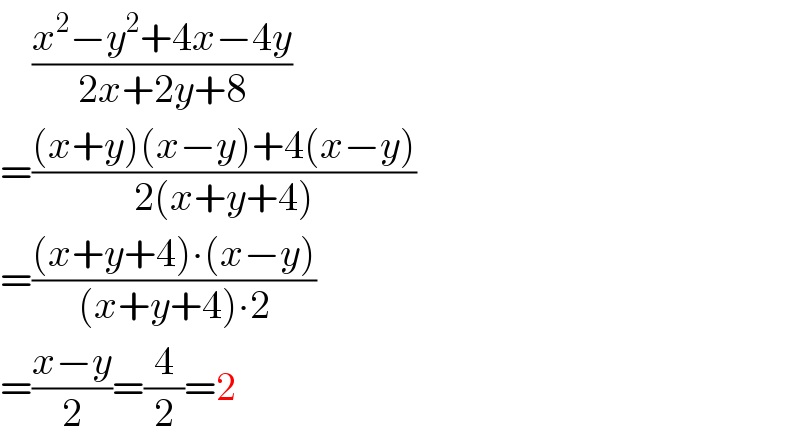
$$\:\:\:\:\frac{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{4}{y}}{\mathrm{2}{x}+\mathrm{2}{y}+\mathrm{8}} \\ $$$$=\frac{\left({x}+{y}\right)\left({x}−{y}\right)+\mathrm{4}\left({x}−{y}\right)}{\mathrm{2}\left({x}+{y}+\mathrm{4}\right)} \\ $$$$=\frac{\left({x}+{y}+\mathrm{4}\right)\centerdot\left({x}−{y}\right)}{\left({x}+{y}+\mathrm{4}\right)\centerdot\mathrm{2}} \\ $$$$=\frac{{x}−{y}}{\mathrm{2}}=\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2} \\ $$
