Question Number 138532 by mathlove last updated on 14/Apr/21
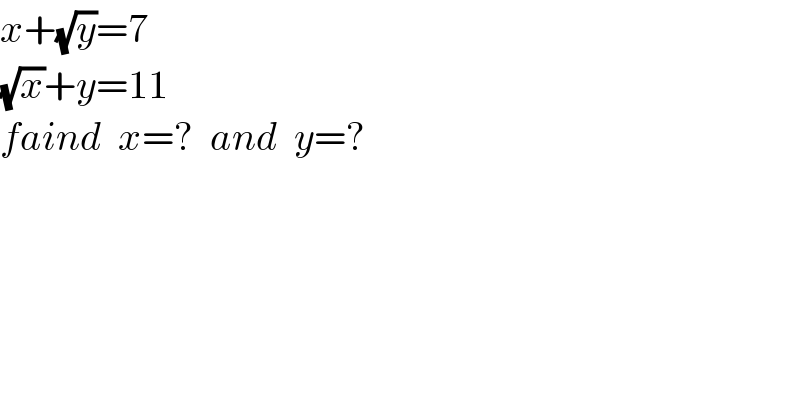
$${x}+\sqrt{{y}}=\mathrm{7} \\ $$$$\sqrt{{x}}+{y}=\mathrm{11} \\ $$$${faind}\:\:{x}=?\:\:{and}\:\:{y}=? \\ $$
Answered by henderson last updated on 14/Apr/21

$$\begin{cases}{{x}\:+\:\sqrt{{y}\:}\:=\:\mathrm{7}}\\{\sqrt{{x}}\:+\:{y}\:=\:\mathrm{11}}\end{cases}\:\Leftrightarrow\:\begin{cases}{{x}\:=\:\mathrm{7}\:−\:\sqrt{{y}}}\\{\sqrt{\mathrm{7}−\sqrt{{y}}}\:+\:{y}\:=\:\mathrm{11}}\end{cases}\:\Leftrightarrow\:\begin{cases}{{x}\:=\:\mathrm{7}−\sqrt{{y}}}\\{\sqrt{\mathrm{7}−\sqrt{{y}}}\:=\:\mathrm{11}−{y}}\end{cases}\Leftrightarrow \\ $$$$\begin{cases}{{x}\:=\:\mathrm{7}−\sqrt{{y}}}\\{\mathrm{7}−\sqrt{{y}}\:=\:\left(\mathrm{11}−{y}\right)^{\mathrm{2}} }\end{cases}\:\Leftrightarrow\:\begin{cases}{{x}\:=\:\mathrm{7}−\sqrt{{y}}}\\{\left(\mathrm{7}−\sqrt{\mathrm{7}}\right)^{\mathrm{2}} \:=\:\left(\mathrm{121}−\mathrm{22}{y}+{y}^{\mathrm{2}} \right)^{\mathrm{2}} }\end{cases}\:\Leftrightarrow\: \\ $$$$\begin{cases}{{x}\:=\:\mathrm{7}−\sqrt{{y}}}\\{{y}^{\mathrm{4}} \:−\:\mathrm{44}{y}^{\mathrm{3}} \:+\:\mathrm{712}{y}^{\mathrm{2}} \:−\:\mathrm{5017}{y}\:+\:\mathrm{12996}\:=\:\mathrm{0}}\end{cases}\:\Leftrightarrow\: \\ $$$$\begin{cases}{{x}\:=\:\mathrm{7}−\sqrt{{y}}}\\{{y}\:=\:\mathrm{9},\:{y}\:\approx\:\mathrm{7},\mathrm{868}…\:\left({rejected}\right),\:{y}\:=\:\mathrm{12},\mathrm{848}….\:\left({rejected}\right),\:{y}\:=\:\mathrm{14},\mathrm{283}…\:\left({rejected}\right)}\end{cases} \\ $$$$\begin{cases}{{x}\:=\:\mathrm{7}−\sqrt{\mathrm{9}}}\\{{y}\:=\:\mathrm{9}}\end{cases}\:\:\Leftrightarrow\begin{array}{|c|}{{x}\:=\:\mathrm{4}\:\boldsymbol{\mathrm{and}}\:{y}\:=\:\mathrm{9}.}\\\hline\end{array} \\ $$$$ \\ $$
Commented by mathlove last updated on 14/Apr/21

$${thank}\:{you} \\ $$
Commented by henderson last updated on 14/Apr/21

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome}\:! \\ $$
Answered by behi83417@gmail.com last updated on 14/Apr/21
![{ (((x−4)+((√y)−3)=0)),((((√x)−2)+(y−9)=0)) :}⇒ ⇒ { ((((√x)−2)((√x)+2)+((√y)−3)=0)),((((√x)−2)+((√y)−3)((√y)+3)=0)) :}⇒ { (((√x)−2=−((√y)−3)((√y)+3))),((⇒−((√y)−3)((√y)+3)((√x)+2)+((√y)−3)=0)) :} ⇒−((√y)−3)[((√y)+3)((√x)+2)−1]=0 ⇒(√y)−3=0⇒(√y)=3⇒y=9 ⇒(√x)−2=−((√y)−3)((√y)+3)=0⇒(√x)−2=0 ⇒(√x)=2⇒x=4⇒ { ((x=4)),((y=9 .■)) :}](https://www.tinkutara.com/question/Q138540.png)
$$\begin{cases}{\left(\mathrm{x}−\mathrm{4}\right)+\left(\sqrt{\mathrm{y}}−\mathrm{3}\right)=\mathrm{0}}\\{\left(\sqrt{\mathrm{x}}−\mathrm{2}\right)+\left(\mathrm{y}−\mathrm{9}\right)=\mathrm{0}}\end{cases}\Rightarrow \\ $$$$\Rightarrow\begin{cases}{\left(\sqrt{\mathrm{x}}−\mathrm{2}\right)\left(\sqrt{\mathrm{x}}+\mathrm{2}\right)+\left(\sqrt{\mathrm{y}}−\mathrm{3}\right)=\mathrm{0}}\\{\left(\sqrt{\mathrm{x}}−\mathrm{2}\right)+\left(\sqrt{\mathrm{y}}−\mathrm{3}\right)\left(\sqrt{\mathrm{y}}+\mathrm{3}\right)=\mathrm{0}}\end{cases}\Rightarrow \\ $$$$\begin{cases}{\sqrt{\mathrm{x}}−\mathrm{2}=−\left(\sqrt{\mathrm{y}}−\mathrm{3}\right)\left(\sqrt{\mathrm{y}}+\mathrm{3}\right)}\\{\Rightarrow−\left(\sqrt{\mathrm{y}}−\mathrm{3}\right)\left(\sqrt{\mathrm{y}}+\mathrm{3}\right)\left(\sqrt{\mathrm{x}}+\mathrm{2}\right)+\left(\sqrt{\mathrm{y}}−\mathrm{3}\right)=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow−\left(\sqrt{\mathrm{y}}−\mathrm{3}\right)\left[\left(\sqrt{\mathrm{y}}+\mathrm{3}\right)\left(\sqrt{\mathrm{x}}+\mathrm{2}\right)−\mathrm{1}\right]=\mathrm{0} \\ $$$$\Rightarrow\sqrt{\mathrm{y}}−\mathrm{3}=\mathrm{0}\Rightarrow\sqrt{\mathrm{y}}=\mathrm{3}\Rightarrow\mathrm{y}=\mathrm{9} \\ $$$$\Rightarrow\sqrt{\mathrm{x}}−\mathrm{2}=−\left(\sqrt{\mathrm{y}}−\mathrm{3}\right)\left(\sqrt{\mathrm{y}}+\mathrm{3}\right)=\mathrm{0}\Rightarrow\sqrt{\mathrm{x}}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\sqrt{\mathrm{x}}=\mathrm{2}\Rightarrow\mathrm{x}=\mathrm{4}\Rightarrow\begin{cases}{\mathrm{x}=\mathrm{4}}\\{\mathrm{y}=\mathrm{9}\:\:\:\:.\blacksquare}\end{cases} \\ $$
Commented by Rasheed.Sindhi last updated on 15/Apr/21

$$\vee\:\cap\overset{\bigstar} { }\subset\in\:\mathrm{sir}! \\ $$
