Menu Close

x-y-gt-0-B-x-y-0-1-t-x-1-1-t-y-1-dt-x-0-t-x-1-e-t-dt-1-show-that-x-gt-0-x-1-x-x-and-lim-n-gt-x-x-1-x-n-n-x-n-1-x-

Tinku Tara
Pin




Question Number 65834 by ~ À ® @ 237 ~ last updated on 04/Aug/19
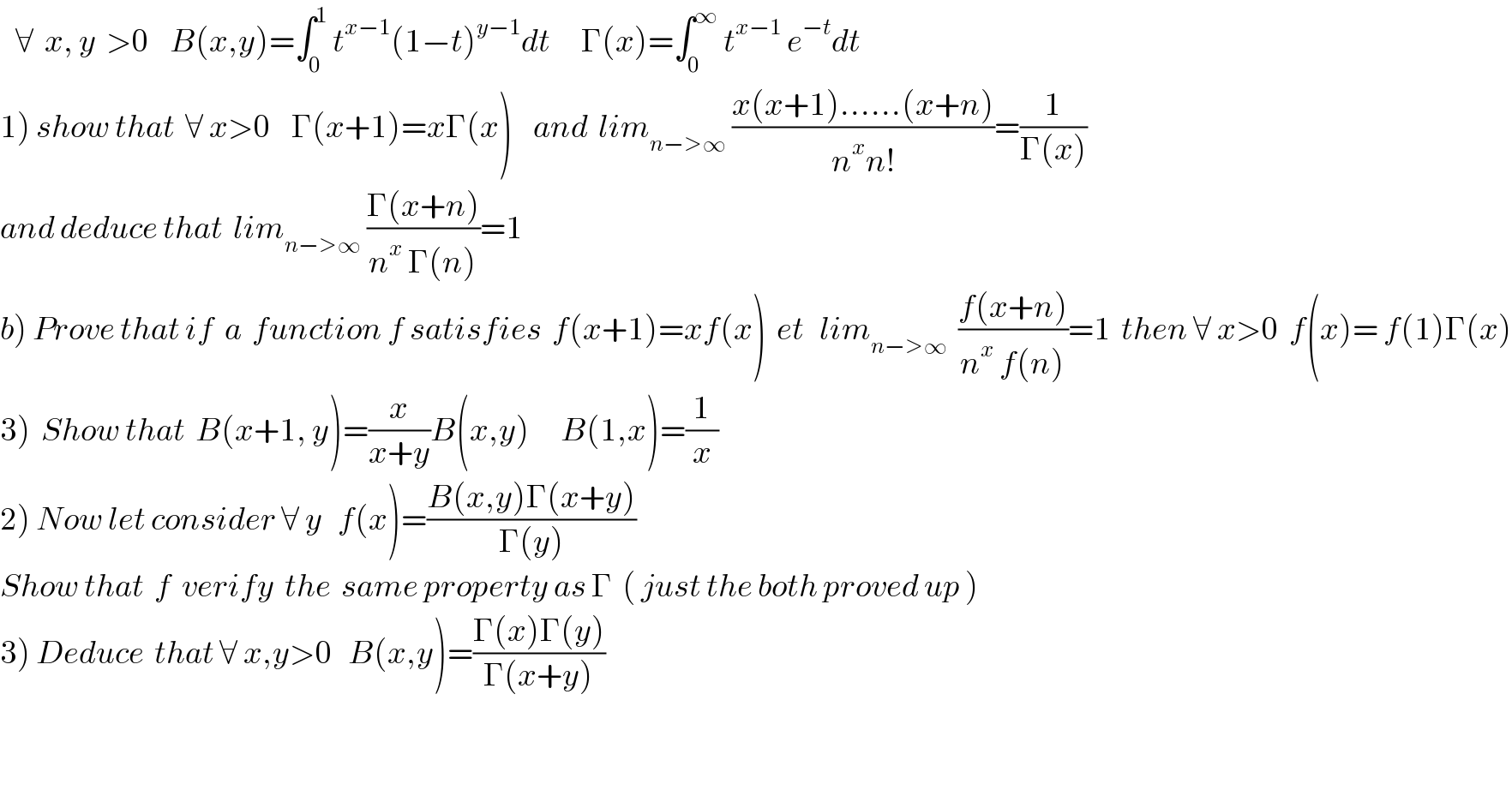
∀ x, y >0 B(x,y)=∫_0 ^1 t^(x−1) (1−t)^(y−1) dt Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) dt 1) show that ∀ x>0 Γ(x+1)=xΓ(x) and lim_(n−>∞) ((x(x+1)......(x+n))/(n^x n!))=(1/(Γ(x))) and deduce that lim_(n−>∞) ((Γ(x+n))/(n^x Γ(n)))=1 b) Prove that if a function f satisfies f(x+1)=xf(x) et lim_(n−>∞) ((f(x+n))/(n^x f(n)))=1 then ∀ x>0 f(x)= f(1)Γ(x) 3) Show that B(x+1, y)=(x/(x+y))B(x,y) B(1,x)=(1/x) 2) Now let consider ∀ y f(x)=((B(x,y)Γ(x+y))/(Γ(y))) Show that f verify the same property as Γ ( just the both proved up ) 3) Deduce that ∀ x,y>0 B(x,y)=((Γ(x)Γ(y))/(Γ(x+y)))
$$\:\:\:\forall\:\:{x},\:{y}\:\:>\mathrm{0}\:\:\:\:{B}\left({x},{y}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{x}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{y}−\mathrm{1}} {dt}\:\:\:\:\:\:\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} \:{e}^{−{t}} {dt} \\ $$$$\left.\mathrm{1}\right)\:{show}\:{that}\:\:\forall\:{x}>\mathrm{0}\:\:\:\:\Gamma\left({x}+\mathrm{1}\right)={x}\Gamma\left({x}\right)\:\:\:\:{and}\:\:{lim}_{{n}−>\infty} \:\frac{{x}\left({x}+\mathrm{1}\right)……\left({x}+{n}\right)}{{n}^{{x}} {n}!}=\frac{\mathrm{1}}{\Gamma\left({x}\right)} \\ $$$${and}\:{deduce}\:{that}\:\:{lim}_{{n}−>\infty} \:\frac{\Gamma\left({x}+{n}\right)}{{n}^{{x}} \:\Gamma\left({n}\right)}=\mathrm{1} \\ $$$$\left.{b}\right)\:{Prove}\:{that}\:{if}\:\:{a}\:\:{function}\:{f}\:{satisfies}\:\:{f}\left({x}+\mathrm{1}\right)={xf}\left({x}\right)\:\:{et}\:\:\:{lim}_{{n}−>\infty} \:\:\frac{{f}\left({x}+{n}\right)}{{n}^{{x}} \:{f}\left({n}\right)}=\mathrm{1}\:\:{then}\:\forall\:{x}>\mathrm{0}\:\:{f}\left({x}\right)=\:{f}\left(\mathrm{1}\right)\Gamma\left({x}\right) \\ $$$$\left.\mathrm{3}\right)\:\:{Show}\:{that}\:\:{B}\left({x}+\mathrm{1},\:{y}\right)=\frac{{x}}{{x}+{y}}{B}\left({x},{y}\right)\:\:\:\:\:\:{B}\left(\mathrm{1},{x}\right)=\frac{\mathrm{1}}{{x}}\: \\ $$$$\left.\mathrm{2}\right)\:{Now}\:{let}\:{consider}\:\forall\:{y}\:\:\:{f}\left({x}\right)=\frac{{B}\left({x},{y}\right)\Gamma\left({x}+{y}\right)}{\Gamma\left({y}\right)}\: \\ $$$${Show}\:{that}\:\:{f}\:\:{verify}\:\:{the}\:\:{same}\:{property}\:{as}\:\Gamma\:\:\left(\:{just}\:{the}\:{both}\:{proved}\:{up}\:\right)\: \\ $$$$\left.\mathrm{3}\right)\:{Deduce}\:\:{that}\:\forall\:{x},{y}>\mathrm{0}\:\:\:{B}\left({x},{y}\right)=\frac{\Gamma\left({x}\right)\Gamma\left({y}\right)}{\Gamma\left({x}+{y}\right)} \\ $$
Commented by mathmax by abdo last updated on 07/Aug/19
1)Γ(x+1)=∫_0 ^∞ t^x e^(−t) dt by parts u =t^x and v^′ =e^(−t) ⇒ Γ(x+1) =[t^x e^(−t) ]_0 ^∞ −∫_0 ^∞ x t^(x−1) (−e^(−t) )dt =x∫_0 ^∞ t^(x−1) e^(−t) dt =xΓ(x) we have e^u =lim_(n→+∞) (1+(u/n))^n ⇒e^(−t) =lim_(n→+∞) (1−(t/n))^n ⇒ Γ(x) =lim_(n→+∞) ∫_0 ^∞ t^(x−1) (1−(t/n))^n dt=lim_(n→+∞) W_n W_n =_(t=nu) ∫_0 ^∞ (nu)^(x−1) (1−u)^n ndu =n^x ∫_0 ^∞ u^(x−1) (1−u)^n du integration by parts chow that ∫_0 ^∞ u^(x−1) (1−u)^n du =((n!)/(x(x+1)....(x+n))) ⇒ Γ(x) =lim_(n→+∞) ((n^x n!)/(x(x+1)(x+2)....(x+n)))
$$\left.\mathrm{1}\right)\Gamma\left({x}+\mathrm{1}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{x}} {e}^{−{t}} {dt}\:\:{by}\:{parts}\:\:{u}\:={t}^{{x}} \:{and}\:{v}^{'} ={e}^{−{t}} \:\Rightarrow \\ $$$$\Gamma\left({x}+\mathrm{1}\right)\:=\left[{t}^{{x}} \:{e}^{−{t}} \right]_{\mathrm{0}} ^{\infty} \:−\int_{\mathrm{0}} ^{\infty} {x}\:{t}^{{x}−\mathrm{1}} \:\left(−{e}^{−{t}} \right){dt}\:={x}\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} \:{e}^{−{t}} {dt} \\ $$$$={x}\Gamma\left({x}\right) \\ $$$${we}\:{have}\:{e}^{{u}} \:={lim}_{{n}\rightarrow+\infty} \left(\mathrm{1}+\frac{{u}}{{n}}\right)^{{n}} \:\Rightarrow{e}^{−{t}} \:={lim}_{{n}\rightarrow+\infty} \left(\mathrm{1}−\frac{{t}}{{n}}\right)^{{n}} \:\Rightarrow \\ $$$$\Gamma\left({x}\right)\:={lim}_{{n}\rightarrow+\infty} \:\:\int_{\mathrm{0}} ^{\infty} \:\:{t}^{{x}−\mathrm{1}} \left(\mathrm{1}−\frac{{t}}{{n}}\right)^{{n}} \:{dt}={lim}_{{n}\rightarrow+\infty} {W}_{{n}} \\ $$$${W}_{{n}} =_{{t}={nu}} \:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\left({nu}\right)^{{x}−\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{n}} {ndu} \\ $$$$={n}^{{x}} \int_{\mathrm{0}} ^{\infty} \:\:{u}^{{x}−\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{n}} \:{du}\:\:\:\:{integration}\:{by}\:{parts}\:{chow}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\infty} {u}^{{x}−\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{n}} {du}\:=\frac{{n}!}{{x}\left({x}+\mathrm{1}\right)….\left({x}+{n}\right)}\:\Rightarrow \\ $$$$\Gamma\left({x}\right)\:={lim}_{{n}\rightarrow+\infty} \:\:\:\frac{{n}^{{x}} {n}!}{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)….\left({x}+{n}\right)} \\ $$

Pin