Question Number 71984 by Henri Boucatchou last updated on 23/Oct/19
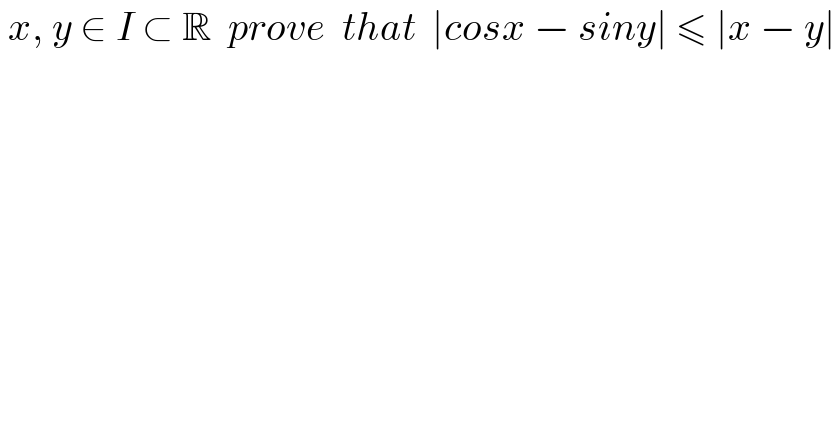
$$\:{x},\:{y}\:\in\:{I}\:\subset\:\mathbb{R}\:\:{prove}\:\:{that}\:\:\mid{cosx}\:−\:{siny}\mid\:\leqslant\:\mid{x}\:−\:{y}\mid \\ $$
Answered by mind is power last updated on 23/Oct/19
![x=y=0 mistack ⇒1≤0 i think is ∣sin(x)−sin(y)∣≤∣x−y∣ letf(x,y)= ∫_x ^y cos(t)dt f(x,y)=[sin(t)]_x ^y =sin(y)−sin(x) ∣f(x,y)∣=∣∫_x ^y cos(t)dt∣≤∣∫_x ^y ∣cos(t)dt∣∣≤∣∫_x ^y 1dt∣=∣y−x∣ ⇒∣sin(y)−sin(x)∣≤∣y−x∣](https://www.tinkutara.com/question/Q72003.png)
$$\mathrm{x}=\mathrm{y}=\mathrm{0}\:\mathrm{mistack} \\ $$$$\Rightarrow\mathrm{1}\leqslant\mathrm{0} \\ $$$$\mathrm{i}\:\mathrm{think}\:\mathrm{is}\:\mid\mathrm{sin}\left(\mathrm{x}\right)−\mathrm{sin}\left(\mathrm{y}\right)\mid\leqslant\mid\mathrm{x}−\mathrm{y}\mid \\ $$$$\mathrm{letf}\left(\mathrm{x},\mathrm{y}\right)=\:\int_{\mathrm{x}} ^{\mathrm{y}} \mathrm{cos}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)=\left[\mathrm{sin}\left(\mathrm{t}\right)\right]_{\mathrm{x}} ^{\mathrm{y}} =\mathrm{sin}\left(\mathrm{y}\right)−\mathrm{sin}\left(\mathrm{x}\right) \\ $$$$\mid\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)\mid=\mid\int_{\mathrm{x}} ^{\mathrm{y}} \mathrm{cos}\left(\mathrm{t}\right)\mathrm{dt}\mid\leqslant\mid\int_{\mathrm{x}} ^{\mathrm{y}} \mid\mathrm{cos}\left(\mathrm{t}\right)\mathrm{dt}\mid\mid\leqslant\mid\int_{\mathrm{x}} ^{\mathrm{y}} \mathrm{1dt}\mid=\mid\mathrm{y}−\mathrm{x}\mid \\ $$$$\Rightarrow\mid\mathrm{sin}\left(\mathrm{y}\right)−\mathrm{sin}\left(\mathrm{x}\right)\mid\leqslant\mid\mathrm{y}−\mathrm{x}\mid \\ $$
Commented by Henri Boucatchou last updated on 23/Oct/19
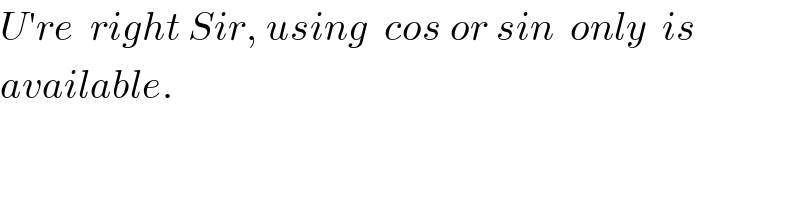
$${U}'{re}\:\:{right}\:{Sir},\:{using}\:\:{cos}\:{or}\:{sin}\:\:{only}\:\:{is} \\ $$$${available}. \\ $$
