Question Number 143776 by akmalovna05 last updated on 18/Jun/21
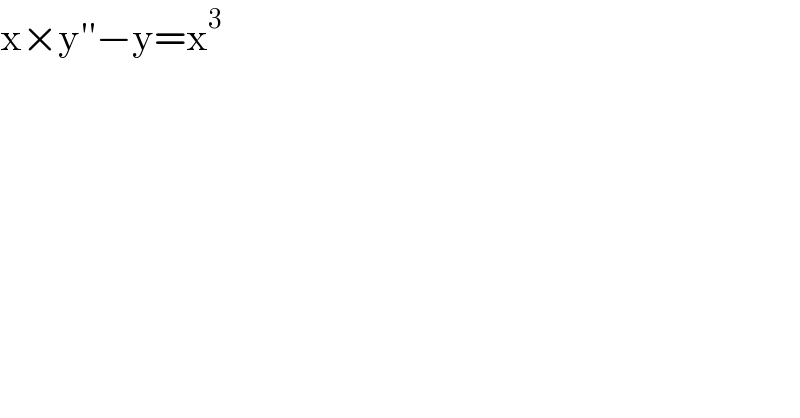
$$\mathrm{x}×\mathrm{y}''−\mathrm{y}=\mathrm{x}^{\mathrm{3}} \\ $$
Answered by Olaf_Thorendsen last updated on 18/Jun/21

$${xy}''−{y}\:=\:{x}^{\mathrm{3}} \:\:\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{Particular}\:\mathrm{solution}\:: \\ $$$${y}\:=\:{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$${y}'\:=\:\mathrm{3}{ax}^{\mathrm{2}} +\mathrm{2}{bx}+{c} \\ $$$${y}''\:=\:\mathrm{6}{ax}+\mathrm{2}{b} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\::\:\mathrm{6}{ax}^{\mathrm{2}} +\mathrm{2}{bx}−{ax}^{\mathrm{3}} −{bx}^{\mathrm{2}} −{cx}−{d}\:=\:{x}^{\mathrm{3}} \\ $$$$\begin{cases}{−{a}\:=\:\mathrm{1}}\\{\mathrm{6}{a}−{b}\:=\:\mathrm{0}}\\{\mathrm{2}{b}−{c}\:=\:\mathrm{0}}\\{−{d}\:=\:\mathrm{0}}\end{cases} \\ $$$${a}\:=\:−\mathrm{1},\:{b}\:=\:−\mathrm{6},\:{c}\:=\:−\mathrm{12},\:{d}\:=\:\mathrm{0} \\ $$$${y}\:=\:−{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} −\mathrm{12}{x} \\ $$$$ \\ $$$$\mathrm{Homogen}\:\mathrm{solution}\:: \\ $$$${xy}''−{y}\:=\:\mathrm{0} \\ $$$$\rightarrow\:\mathrm{see}\:\mathrm{Bessel}\:\mathrm{equation} \\ $$$$ \\ $$
Commented by SANOGO last updated on 30/Aug/21

