x-y-z-1-x-2-y-2-z-2-2-x-3-y-3-z-3-3-find-x-4-y-4-z-4-x-5-y-5-z-5-x-6-y-6-z-6-x-n-y-n-z-n-

Question Number 74970 by mr W last updated on 05/Dec/19

$${x}+{y}+{z}=\mathrm{1} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{2} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} =\mathrm{3} \\ $$$$ \\ $$$${find} \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} =? \\ $$$${x}^{\mathrm{5}} +{y}^{\mathrm{5}} +{z}^{\mathrm{5}} =? \\ $$$${x}^{\mathrm{6}} +{y}^{\mathrm{6}} +{z}^{\mathrm{6}} =? \\ $$$$…… \\ $$$${x}^{{n}} +{y}^{{n}} +{z}^{{n}} =? \\ $$

Commented by TawaTawa last updated on 05/Dec/19

$$\mathrm{Wow},\:\:\mathrm{i}\:\mathrm{will}\:\mathrm{love}\:\mathrm{to}\:\mathrm{see}\:\mathrm{the}\:\mathrm{answer}.\: \\ $$

Commented by mr W last updated on 05/Dec/19

Commented by mr W last updated on 05/Dec/19

Commented by mr W last updated on 05/Dec/19

https://en.m.wikipedia.org/wiki/Newton%27s_identities

Commented by mr W last updated on 05/Dec/19

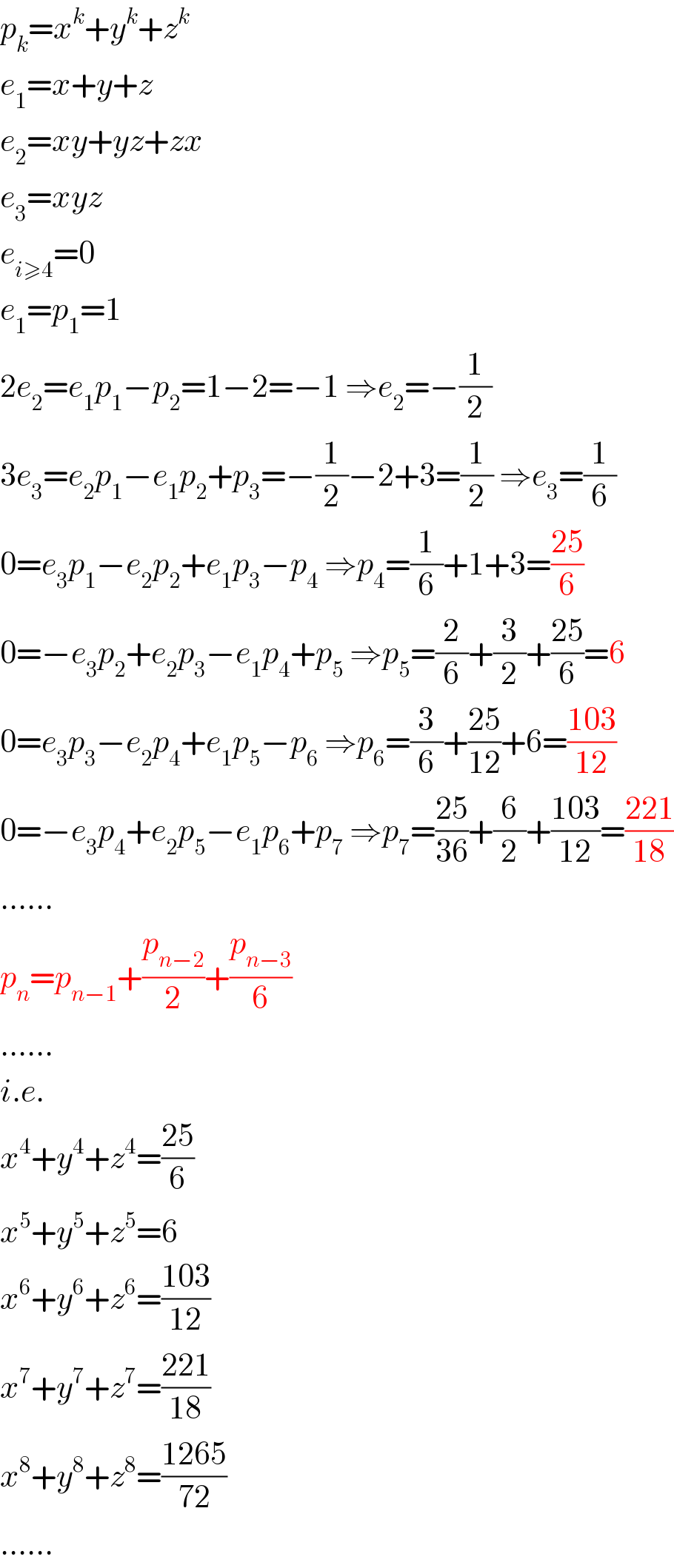
p_k =x^k +y^k +z^k e_1 =x+y+z e_2 =xy+yz+zx e_3 =xyz e_(i≥4) =0 e_1 =p_1 =1 2e_2 =e_1 p_1 −p_2 =1−2=−1 ⇒e_2 =−(1/2) 3e_3 =e_2 p_1 −e_1 p_2 +p_3 =−(1/2)−2+3=(1/2) ⇒e_3 =(1/6) 0=e_3 p_1 −e_2 p_2 +e_1 p_3 −p_4 ⇒p_4 =(1/6)+1+3=((25)/6) 0=−e_3 p_2 +e_2 p_3 −e_1 p_4 +p_5 ⇒p_5 =(2/6)+(3/2)+((25)/6)=6 0=e_3 p_3 −e_2 p_4 +e_1 p_5 −p_6 ⇒p_6 =(3/6)+((25)/(12))+6=((103)/(12)) 0=−e_3 p_4 +e_2 p_5 −e_1 p_6 +p_7 ⇒p_7 =((25)/(36))+(6/2)+((103)/(12))=((221)/(18)) ...... p_n =p_(n−1) +(p_(n−2) /2)+(p_(n−3) /6) ...... i.e. x^4 +y^4 +z^4 =((25)/6) x^5 +y^5 +z^5 =6 x^6 +y^6 +z^6 =((103)/(12)) x^7 +y^7 +z^7 =((221)/(18)) x^8 +y^8 +z^8 =((1265)/(72)) ......

$${p}_{{k}} ={x}^{{k}} +{y}^{{k}} +{z}^{{k}} \\ $$$${e}_{\mathrm{1}} ={x}+{y}+{z} \\ $$$${e}_{\mathrm{2}} ={xy}+{yz}+{zx} \\ $$$${e}_{\mathrm{3}} ={xyz} \\ $$$${e}_{{i}\geqslant\mathrm{4}} =\mathrm{0} \\ $$$${e}_{\mathrm{1}} ={p}_{\mathrm{1}} =\mathrm{1} \\ $$$$\mathrm{2}{e}_{\mathrm{2}} ={e}_{\mathrm{1}} {p}_{\mathrm{1}} −{p}_{\mathrm{2}} =\mathrm{1}−\mathrm{2}=−\mathrm{1}\:\Rightarrow{e}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{3}{e}_{\mathrm{3}} ={e}_{\mathrm{2}} {p}_{\mathrm{1}} −{e}_{\mathrm{1}} {p}_{\mathrm{2}} +{p}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}+\mathrm{3}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{e}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\mathrm{0}={e}_{\mathrm{3}} {p}_{\mathrm{1}} −{e}_{\mathrm{2}} {p}_{\mathrm{2}} +{e}_{\mathrm{1}} {p}_{\mathrm{3}} −{p}_{\mathrm{4}} \:\Rightarrow{p}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{6}}+\mathrm{1}+\mathrm{3}=\frac{\mathrm{25}}{\mathrm{6}} \\ $$$$\mathrm{0}=−{e}_{\mathrm{3}} {p}_{\mathrm{2}} +{e}_{\mathrm{2}} {p}_{\mathrm{3}} −{e}_{\mathrm{1}} {p}_{\mathrm{4}} +{p}_{\mathrm{5}} \:\Rightarrow{p}_{\mathrm{5}} =\frac{\mathrm{2}}{\mathrm{6}}+\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{25}}{\mathrm{6}}=\mathrm{6} \\ $$$$\mathrm{0}={e}_{\mathrm{3}} {p}_{\mathrm{3}} −{e}_{\mathrm{2}} {p}_{\mathrm{4}} +{e}_{\mathrm{1}} {p}_{\mathrm{5}} −{p}_{\mathrm{6}} \:\Rightarrow{p}_{\mathrm{6}} =\frac{\mathrm{3}}{\mathrm{6}}+\frac{\mathrm{25}}{\mathrm{12}}+\mathrm{6}=\frac{\mathrm{103}}{\mathrm{12}} \\ $$$$\mathrm{0}=−{e}_{\mathrm{3}} {p}_{\mathrm{4}} +{e}_{\mathrm{2}} {p}_{\mathrm{5}} −{e}_{\mathrm{1}} {p}_{\mathrm{6}} +{p}_{\mathrm{7}} \:\Rightarrow{p}_{\mathrm{7}} =\frac{\mathrm{25}}{\mathrm{36}}+\frac{\mathrm{6}}{\mathrm{2}}+\frac{\mathrm{103}}{\mathrm{12}}=\frac{\mathrm{221}}{\mathrm{18}} \\ $$$$…… \\ $$$${p}_{{n}} ={p}_{{n}−\mathrm{1}} +\frac{{p}_{{n}−\mathrm{2}} }{\mathrm{2}}+\frac{{p}_{{n}−\mathrm{3}} }{\mathrm{6}} \\ $$$$…… \\ $$$${i}.{e}. \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} =\frac{\mathrm{25}}{\mathrm{6}} \\ $$$${x}^{\mathrm{5}} +{y}^{\mathrm{5}} +{z}^{\mathrm{5}} =\mathrm{6} \\ $$$${x}^{\mathrm{6}} +{y}^{\mathrm{6}} +{z}^{\mathrm{6}} =\frac{\mathrm{103}}{\mathrm{12}} \\ $$$${x}^{\mathrm{7}} +{y}^{\mathrm{7}} +{z}^{\mathrm{7}} =\frac{\mathrm{221}}{\mathrm{18}} \\ $$$${x}^{\mathrm{8}} +{y}^{\mathrm{8}} +{z}^{\mathrm{8}} =\frac{\mathrm{1265}}{\mathrm{72}} \\ $$$$…… \\ $$

Commented by TawaTawa last updated on 05/Dec/19

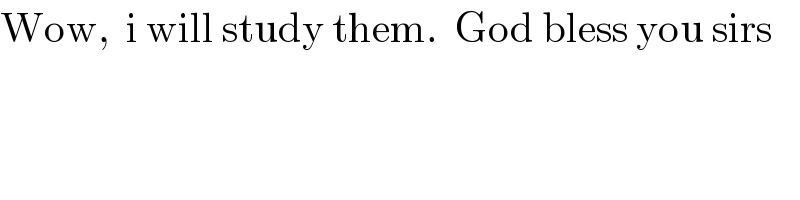
Wow, i will study them. God bless you sirs

$$\mathrm{Wow},\:\:\mathrm{i}\:\mathrm{will}\:\mathrm{study}\:\mathrm{them}.\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sirs} \\ $$

Commented by TawaTawa last updated on 05/Dec/19

The only thing i don′t understand is how to get 2e_2 , 3e_3 , 4e_4 , 5e_5 , etc... Please help

$$\mathrm{The}\:\mathrm{only}\:\mathrm{thing}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{is}\:\mathrm{how}\:\mathrm{to}\:\mathrm{get} \\ $$$$\mathrm{2e}_{\mathrm{2}} \:,\:\:\mathrm{3e}_{\mathrm{3}} \:,\:\:\:\mathrm{4e}_{\mathrm{4}} \:,\:\:\:\mathrm{5e}_{\mathrm{5}} \:,\:\:\:\:\:\mathrm{etc}… \\ $$$$\mathrm{Please}\:\mathrm{help} \\ $$

Commented by mind is power last updated on 05/Dec/19

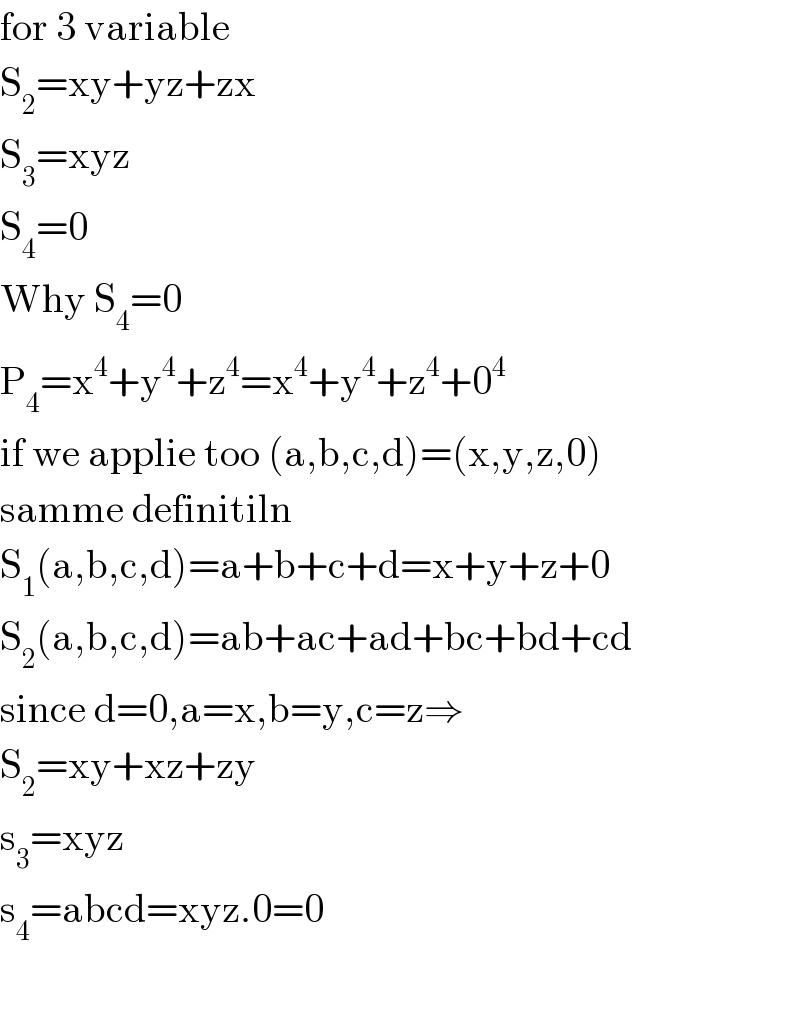
for 3 variable S_2 =xy+yz+zx S_3 =xyz S_4 =0 Why S_4 =0 P_4 =x^4 +y^4 +z^4 =x^4 +y^4 +z^4 +0^4 if we applie too (a,b,c,d)=(x,y,z,0) samme definitiln S_1 (a,b,c,d)=a+b+c+d=x+y+z+0 S_2 (a,b,c,d)=ab+ac+ad+bc+bd+cd since d=0,a=x,b=y,c=z⇒ S_2 =xy+xz+zy s_3 =xyz s_4 =abcd=xyz.0=0

$$\mathrm{for}\:\mathrm{3}\:\mathrm{variable} \\ $$$$\mathrm{S}_{\mathrm{2}} =\mathrm{xy}+\mathrm{yz}+\mathrm{zx} \\ $$$$\mathrm{S}_{\mathrm{3}} =\mathrm{xyz} \\ $$$$\mathrm{S}_{\mathrm{4}} =\mathrm{0} \\ $$$$\mathrm{Why}\:\mathrm{S}_{\mathrm{4}} =\mathrm{0} \\ $$$$\mathrm{P}_{\mathrm{4}} =\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} +\mathrm{z}^{\mathrm{4}} =\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} +\mathrm{z}^{\mathrm{4}} +\mathrm{0}^{\mathrm{4}} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{applie}\:\mathrm{too}\:\left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\right)=\left(\mathrm{x},\mathrm{y},\mathrm{z},\mathrm{0}\right)\: \\ $$$$\mathrm{samme}\:\mathrm{definitiln} \\ $$$$\mathrm{S}_{\mathrm{1}} \left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\right)=\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}=\mathrm{x}+\mathrm{y}+\mathrm{z}+\mathrm{0} \\ $$$$\mathrm{S}_{\mathrm{2}} \left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\right)=\mathrm{ab}+\mathrm{ac}+\mathrm{ad}+\mathrm{bc}+\mathrm{bd}+\mathrm{cd} \\ $$$$\mathrm{since}\:\mathrm{d}=\mathrm{0},\mathrm{a}=\mathrm{x},\mathrm{b}=\mathrm{y},\mathrm{c}=\mathrm{z}\Rightarrow \\ $$$$\mathrm{S}_{\mathrm{2}} =\mathrm{xy}+\mathrm{xz}+\mathrm{zy} \\ $$$$\mathrm{s}_{\mathrm{3}} =\mathrm{xyz} \\ $$$$\mathrm{s}_{\mathrm{4}} =\mathrm{abcd}=\mathrm{xyz}.\mathrm{0}=\mathrm{0} \\ $$$$ \\ $$

Commented by TawaTawa last updated on 05/Dec/19

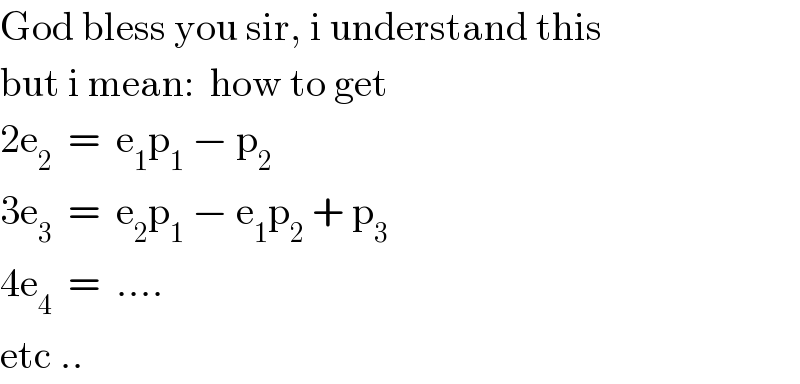
God bless you sir, i understand this but i mean: how to get 2e_2 = e_1 p_1 − p_2 3e_3 = e_2 p_1 − e_1 p_2 + p_3 4e_4 = .... etc ..

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{understand}\:\mathrm{this} \\ $$$$\mathrm{but}\:\mathrm{i}\:\mathrm{mean}:\:\:\mathrm{how}\:\mathrm{to}\:\mathrm{get} \\ $$$$\mathrm{2e}_{\mathrm{2}} \:\:=\:\:\mathrm{e}_{\mathrm{1}} \mathrm{p}_{\mathrm{1}} \:−\:\mathrm{p}_{\mathrm{2}} \\ $$$$\mathrm{3e}_{\mathrm{3}} \:\:=\:\:\mathrm{e}_{\mathrm{2}} \mathrm{p}_{\mathrm{1}} \:−\:\mathrm{e}_{\mathrm{1}} \mathrm{p}_{\mathrm{2}} \:+\:\mathrm{p}_{\mathrm{3}} \\ $$$$\mathrm{4e}_{\mathrm{4}} \:\:=\:\:….\: \\ $$$$\mathrm{etc}\:.. \\ $$

Commented by mind is power last updated on 05/Dec/19

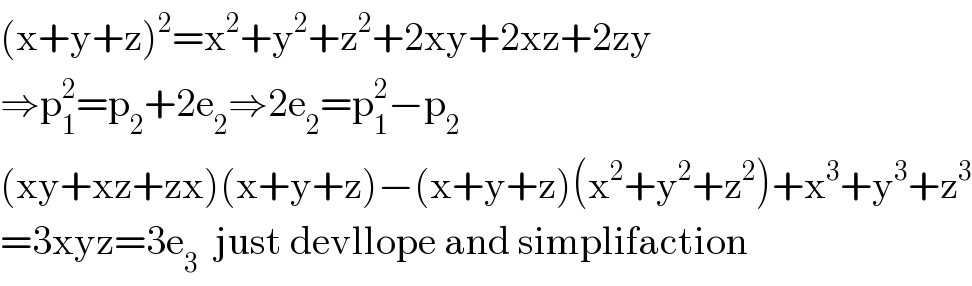
(x+y+z)^2 =x^2 +y^2 +z^2 +2xy+2xz+2zy ⇒p_1 ^2 =p_2 +2e_2 ⇒2e_2 =p_1 ^2 −p_2 (xy+xz+zx)(x+y+z)−(x+y+z)(x^2 +y^2 +z^2 )+x^3 +y^3 +z^3 =3xyz=3e_3 just devllope and simplifaction

$$\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{2xz}+\mathrm{2zy} \\ $$$$\Rightarrow\mathrm{p}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{p}_{\mathrm{2}} +\mathrm{2e}_{\mathrm{2}} \Rightarrow\mathrm{2e}_{\mathrm{2}} =\mathrm{p}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{p}_{\mathrm{2}} \\ $$$$\left(\mathrm{xy}+\mathrm{xz}+\mathrm{zx}\right)\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)−\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \right)+\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} +\mathrm{z}^{\mathrm{3}} \\ $$$$=\mathrm{3xyz}=\mathrm{3e}_{\mathrm{3}} \:\:\mathrm{just}\:\mathrm{devllope}\:\mathrm{and}\:\mathrm{simplifaction} \\ $$

Commented by TawaTawa last updated on 05/Dec/19

$$\mathrm{I}\:\mathrm{understand}\:\mathrm{now}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by mind is power last updated on 05/Dec/19

$$\mathrm{withe}\:\mathrm{pleasur}\:\mathrm{Sir} \\ $$

Commented by Tawa11 last updated on 23/Jul/21

$$\mathrm{Great}.\:\mathrm{I}\:\mathrm{found}\:\mathrm{it}. \\ $$

Answered by MJS last updated on 05/Dec/19

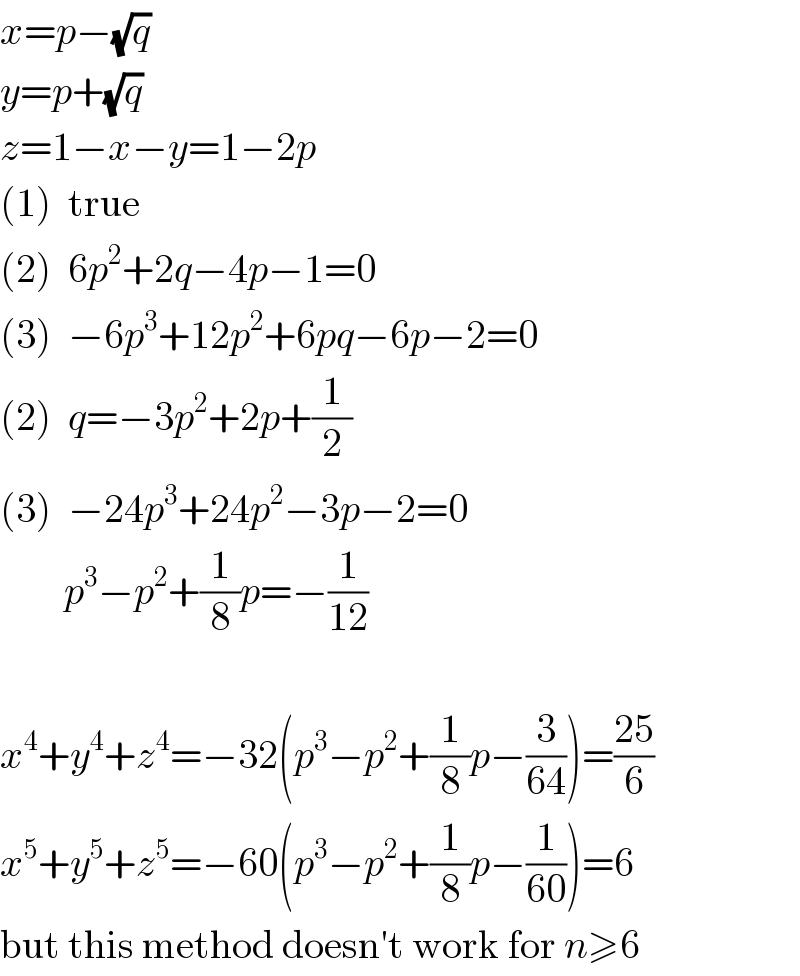
x=p−(√q) y=p+(√q) z=1−x−y=1−2p (1) true (2) 6p^2 +2q−4p−1=0 (3) −6p^3 +12p^2 +6pq−6p−2=0 (2) q=−3p^2 +2p+(1/2) (3) −24p^3 +24p^2 −3p−2=0 p^3 −p^2 +(1/8)p=−(1/(12)) x^4 +y^4 +z^4 =−32(p^3 −p^2 +(1/8)p−(3/(64)))=((25)/6) x^5 +y^5 +z^5 =−60(p^3 −p^2 +(1/8)p−(1/(60)))=6 but this method doesn′t work for n≥6

$${x}={p}−\sqrt{{q}} \\ $$$${y}={p}+\sqrt{{q}} \\ $$$${z}=\mathrm{1}−{x}−{y}=\mathrm{1}−\mathrm{2}{p} \\ $$$$\left(\mathrm{1}\right)\:\:\mathrm{true} \\ $$$$\left(\mathrm{2}\right)\:\:\mathrm{6}{p}^{\mathrm{2}} +\mathrm{2}{q}−\mathrm{4}{p}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\:−\mathrm{6}{p}^{\mathrm{3}} +\mathrm{12}{p}^{\mathrm{2}} +\mathrm{6}{pq}−\mathrm{6}{p}−\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\:{q}=−\mathrm{3}{p}^{\mathrm{2}} +\mathrm{2}{p}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)\:\:−\mathrm{24}{p}^{\mathrm{3}} +\mathrm{24}{p}^{\mathrm{2}} −\mathrm{3}{p}−\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{p}^{\mathrm{3}} −{p}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{8}}{p}=−\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$ \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} =−\mathrm{32}\left({p}^{\mathrm{3}} −{p}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{8}}{p}−\frac{\mathrm{3}}{\mathrm{64}}\right)=\frac{\mathrm{25}}{\mathrm{6}} \\ $$$${x}^{\mathrm{5}} +{y}^{\mathrm{5}} +{z}^{\mathrm{5}} =−\mathrm{60}\left({p}^{\mathrm{3}} −{p}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{8}}{p}−\frac{\mathrm{1}}{\mathrm{60}}\right)=\mathrm{6} \\ $$$$\mathrm{but}\:\mathrm{this}\:\mathrm{method}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{work}\:\mathrm{for}\:{n}\geqslant\mathrm{6} \\ $$

Commented by mr W last updated on 05/Dec/19

$${thanks}\:{alot}\:{sir}! \\ $$

Answered by mind is power last updated on 05/Dec/19

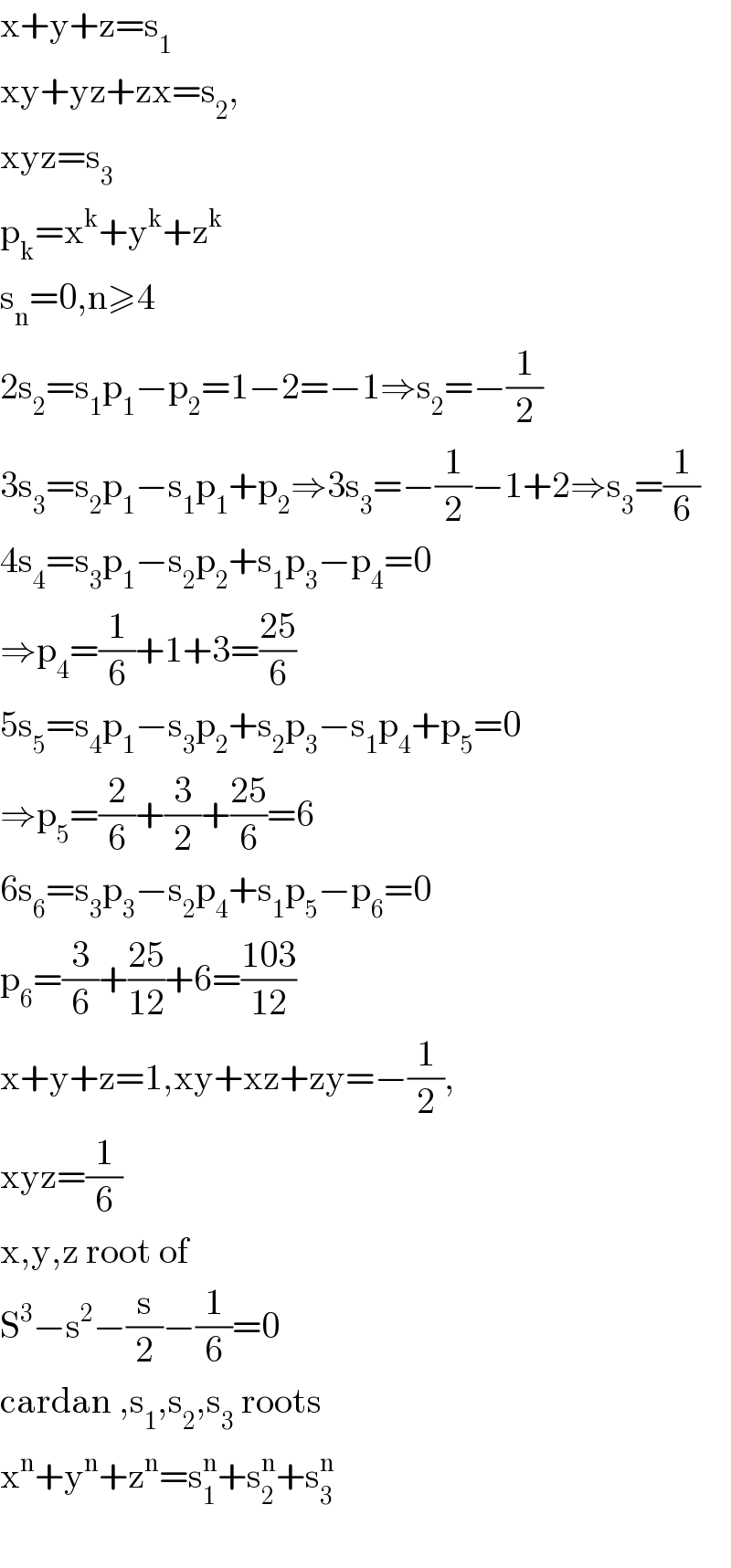
x+y+z=s_1 xy+yz+zx=s_2 , xyz=s_3 p_k =x^k +y^k +z^k s_n =0,n≥4 2s_2 =s_1 p_1 −p_2 =1−2=−1⇒s_2 =−(1/2) 3s_3 =s_2 p_1 −s_1 p_1 +p_2 ⇒3s_3 =−(1/2)−1+2⇒s_3 =(1/6) 4s_4 =s_3 p_1 −s_2 p_2 +s_1 p_3 −p_4 =0 ⇒p_4 =(1/6)+1+3=((25)/6) 5s_5 =s_4 p_1 −s_3 p_2 +s_2 p_3 −s_1 p_4 +p_5 =0 ⇒p_5 =(2/6)+(3/2)+((25)/6)=6 6s_6 =s_3 p_3 −s_2 p_4 +s_1 p_5 −p_6 =0 p_6 =(3/6)+((25)/(12))+6=((103)/(12)) x+y+z=1,xy+xz+zy=−(1/2), xyz=(1/6) x,y,z root of S^3 −s^2 −(s/2)−(1/6)=0 cardan ,s_1 ,s_2 ,s_3 roots x^n +y^n +z^n =s_1 ^n +s_2 ^n +s_3 ^n

$$\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{s}_{\mathrm{1}} \:\:\:\:\:\:\: \\ $$$$\mathrm{xy}+\mathrm{yz}+\mathrm{zx}=\mathrm{s}_{\mathrm{2}} , \\ $$$$\mathrm{xyz}=\mathrm{s}_{\mathrm{3}} \\ $$$$\mathrm{p}_{\mathrm{k}} =\mathrm{x}^{\mathrm{k}} +\mathrm{y}^{\mathrm{k}} +\mathrm{z}^{\mathrm{k}} \\ $$$$\mathrm{s}_{\mathrm{n}} =\mathrm{0},\mathrm{n}\geqslant\mathrm{4} \\ $$$$\mathrm{2s}_{\mathrm{2}} =\mathrm{s}_{\mathrm{1}} \mathrm{p}_{\mathrm{1}} −\mathrm{p}_{\mathrm{2}} =\mathrm{1}−\mathrm{2}=−\mathrm{1}\Rightarrow\mathrm{s}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{3s}_{\mathrm{3}} =\mathrm{s}_{\mathrm{2}} \mathrm{p}_{\mathrm{1}} −\mathrm{s}_{\mathrm{1}} \mathrm{p}_{\mathrm{1}} +\mathrm{p}_{\mathrm{2}} \Rightarrow\mathrm{3s}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}+\mathrm{2}\Rightarrow\mathrm{s}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\mathrm{4s}_{\mathrm{4}} =\mathrm{s}_{\mathrm{3}} \mathrm{p}_{\mathrm{1}} −\mathrm{s}_{\mathrm{2}} \mathrm{p}_{\mathrm{2}} +\mathrm{s}_{\mathrm{1}} \mathrm{p}_{\mathrm{3}} −\mathrm{p}_{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{p}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{6}}+\mathrm{1}+\mathrm{3}=\frac{\mathrm{25}}{\mathrm{6}} \\ $$$$\mathrm{5s}_{\mathrm{5}} =\mathrm{s}_{\mathrm{4}} \mathrm{p}_{\mathrm{1}} −\mathrm{s}_{\mathrm{3}} \mathrm{p}_{\mathrm{2}} +\mathrm{s}_{\mathrm{2}} \mathrm{p}_{\mathrm{3}} −\mathrm{s}_{\mathrm{1}} \mathrm{p}_{\mathrm{4}} +\mathrm{p}_{\mathrm{5}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{p}_{\mathrm{5}} =\frac{\mathrm{2}}{\mathrm{6}}+\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{25}}{\mathrm{6}}=\mathrm{6} \\ $$$$\mathrm{6s}_{\mathrm{6}} =\mathrm{s}_{\mathrm{3}} \mathrm{p}_{\mathrm{3}} −\mathrm{s}_{\mathrm{2}} \mathrm{p}_{\mathrm{4}} +\mathrm{s}_{\mathrm{1}} \mathrm{p}_{\mathrm{5}} −\mathrm{p}_{\mathrm{6}} =\mathrm{0} \\ $$$$\mathrm{p}_{\mathrm{6}} =\frac{\mathrm{3}}{\mathrm{6}}+\frac{\mathrm{25}}{\mathrm{12}}+\mathrm{6}=\frac{\mathrm{103}}{\mathrm{12}} \\ $$$$\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{1},\mathrm{xy}+\mathrm{xz}+\mathrm{zy}=−\frac{\mathrm{1}}{\mathrm{2}}, \\ $$$$\mathrm{xyz}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\mathrm{x},\mathrm{y},\mathrm{z}\:\mathrm{root}\:\mathrm{of} \\ $$$$\mathrm{S}^{\mathrm{3}} −\mathrm{s}^{\mathrm{2}} −\frac{\mathrm{s}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6}}=\mathrm{0} \\ $$$$\mathrm{cardan}\:,\mathrm{s}_{\mathrm{1}} ,\mathrm{s}_{\mathrm{2}} ,\mathrm{s}_{\mathrm{3}} \:\mathrm{roots} \\ $$$$\mathrm{x}^{\mathrm{n}} +\mathrm{y}^{\mathrm{n}} +\mathrm{z}^{\mathrm{n}} =\mathrm{s}_{\mathrm{1}} ^{\mathrm{n}} +\mathrm{s}_{\mathrm{2}} ^{\mathrm{n}} +\mathrm{s}_{\mathrm{3}} ^{\mathrm{n}} \\ $$$$ \\ $$

Commented by mr W last updated on 05/Dec/19