Menu Close

x-y-z-6-xy-xz-yz-11-xyz-6-then-wbat-are-thd-value-of-x-yand-z-

Tinku Tara 0 Comments
Pin




Question Number 9189 by raj bunsha last updated on 22/Nov/16
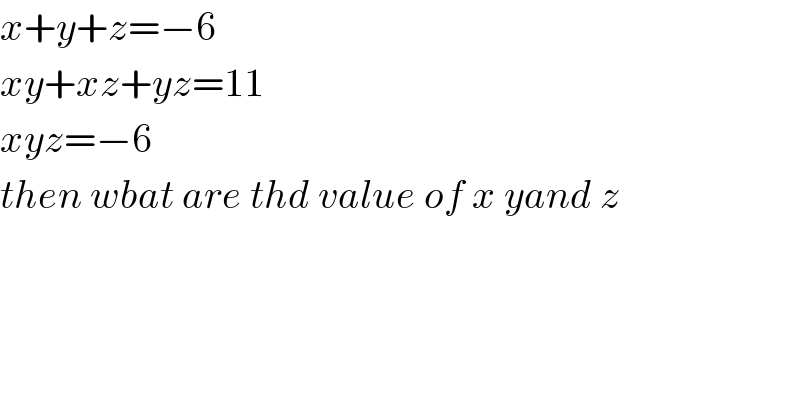
x+y+z=−6 xy+xz+yz=11 xyz=−6 then wbat are thd value of x yand z
x+y+z=−6xy+xz+yz=11xyz=−6thenwbatarethdvalueofxyandz
Answered by mrW last updated on 22/Nov/16
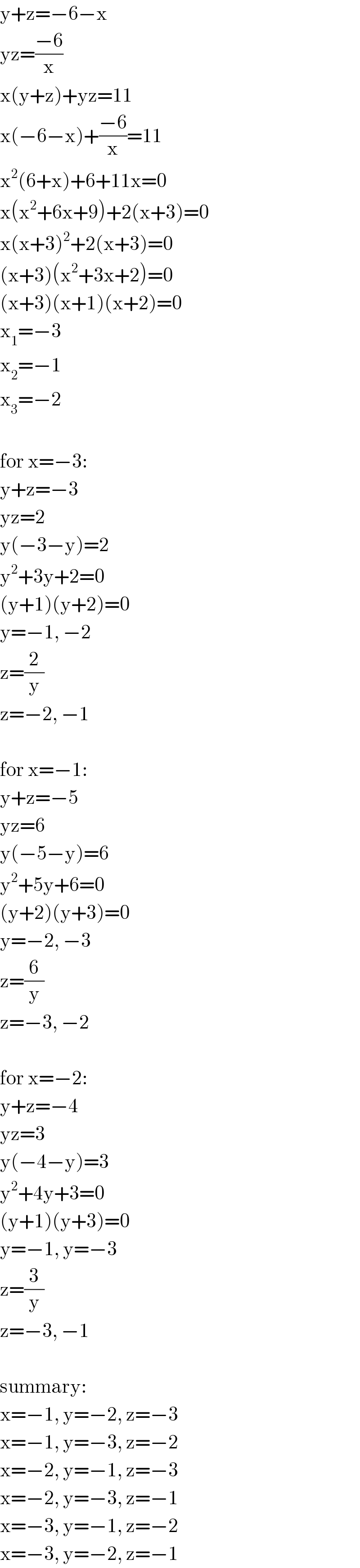
y+z=−6−x yz=((−6)/x) x(y+z)+yz=11 x(−6−x)+((−6)/x)=11 x^2 (6+x)+6+11x=0 x(x^2 +6x+9)+2(x+3)=0 x(x+3)^2 +2(x+3)=0 (x+3)(x^2 +3x+2)=0 (x+3)(x+1)(x+2)=0 x_1 =−3 x_2 =−1 x_3 =−2 for x=−3: y+z=−3 yz=2 y(−3−y)=2 y^2 +3y+2=0 (y+1)(y+2)=0 y=−1, −2 z=(2/y) z=−2, −1 for x=−1: y+z=−5 yz=6 y(−5−y)=6 y^2 +5y+6=0 (y+2)(y+3)=0 y=−2, −3 z=(6/y) z=−3, −2 for x=−2: y+z=−4 yz=3 y(−4−y)=3 y^2 +4y+3=0 (y+1)(y+3)=0 y=−1, y=−3 z=(3/y) z=−3, −1 summary: x=−1, y=−2, z=−3 x=−1, y=−3, z=−2 x=−2, y=−1, z=−3 x=−2, y=−3, z=−1 x=−3, y=−1, z=−2 x=−3, y=−2, z=−1
y+z=−6−xyz=−6xx(y+z)+yz=11x(−6−x)+−6x=11x2(6+x)+6+11x=0x(x2+6x+9)+2(x+3)=0x(x+3)2+2(x+3)=0(x+3)(x2+3x+2)=0(x+3)(x+1)(x+2)=0x1=−3x2=−1x3=−2forx=−3:y+z=−3yz=2y(−3−y)=2y2+3y+2=0(y+1)(y+2)=0y=−1,−2z=2yz=−2,−1forx=−1:y+z=−5yz=6y(−5−y)=6y2+5y+6=0(y+2)(y+3)=0y=−2,−3z=6yz=−3,−2forx=−2:y+z=−4yz=3y(−4−y)=3y2+4y+3=0(y+1)(y+3)=0y=−1,y=−3z=3yz=−3,−1summary:x=−1,y=−2,z=−3x=−1,y=−3,z=−2x=−2,y=−1,z=−3x=−2,y=−3,z=−1x=−3,y=−1,z=−2x=−3,y=−2,z=−1

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *