Question Number 139762 by mathdanisur last updated on 01/May/21
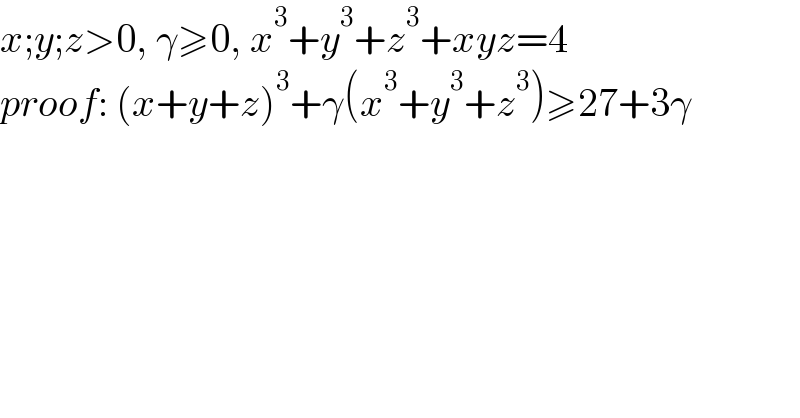
$${x};{y};{z}>\mathrm{0},\:\gamma\geqslant\mathrm{0},\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} +{xyz}=\mathrm{4} \\ $$$${proof}:\:\left({x}+{y}+{z}\right)^{\mathrm{3}} +\gamma\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} \right)\geqslant\mathrm{27}+\mathrm{3}\gamma \\ $$
Answered by mindispower last updated on 02/May/21
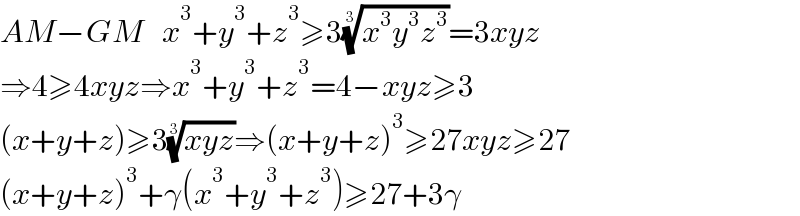
$${AM}−{GM}\:\:\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} \geqslant\mathrm{3}\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} {y}^{\mathrm{3}} {z}^{\mathrm{3}} }=\mathrm{3}{xyz} \\ $$$$\Rightarrow\mathrm{4}\geqslant\mathrm{4}{xyz}\Rightarrow{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} =\mathrm{4}−{xyz}\geqslant\mathrm{3} \\ $$$$\left({x}+{y}+{z}\right)\geqslant\mathrm{3}\sqrt[{\mathrm{3}}]{{xyz}}\Rightarrow\left({x}+{y}+{z}\right)^{\mathrm{3}} \geqslant\mathrm{27}{xyz}\geqslant\mathrm{27} \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{3}} +\gamma\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} \right)\geqslant\mathrm{27}+\mathrm{3}\gamma \\ $$
Commented by mathdanisur last updated on 02/May/21
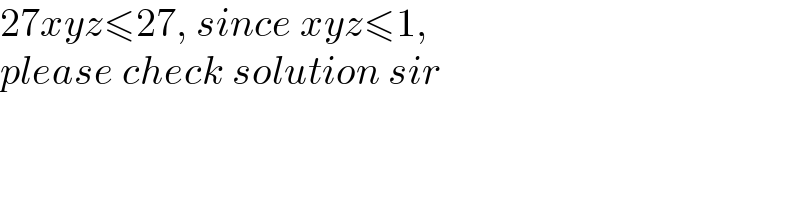
$$\mathrm{27}{xyz}\leqslant\mathrm{27},\:{since}\:{xyz}\leqslant\mathrm{1}, \\ $$$${please}\:{check}\:{solution}\:{sir} \\ $$
