Question Number 75845 by behi83417@gmail.com last updated on 18/Dec/19
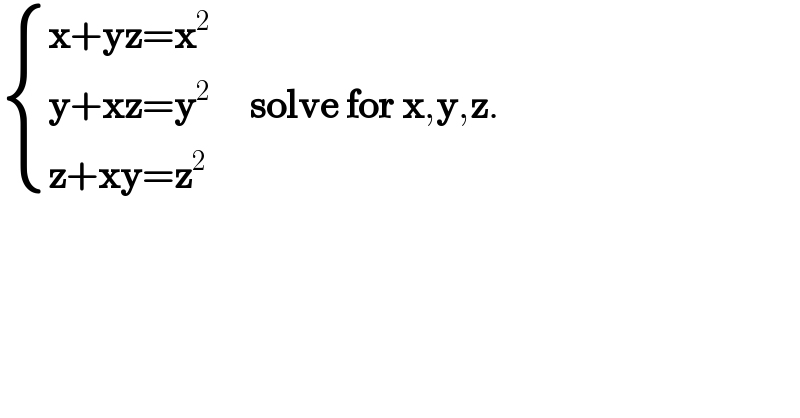
$$\begin{cases}{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{yz}}=\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\\{\boldsymbol{\mathrm{y}}+\boldsymbol{\mathrm{xz}}=\boldsymbol{\mathrm{y}}^{\mathrm{2}} }\\{\boldsymbol{\mathrm{z}}+\boldsymbol{\mathrm{xy}}=\boldsymbol{\mathrm{z}}^{\mathrm{2}} }\end{cases}\:\:\:\:\:\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}},\boldsymbol{\mathrm{z}}. \\ $$
Commented by mr W last updated on 18/Dec/19

$${x}={y}={z}=\mathrm{0} \\ $$
Commented by behi83417@gmail.com last updated on 18/Dec/19
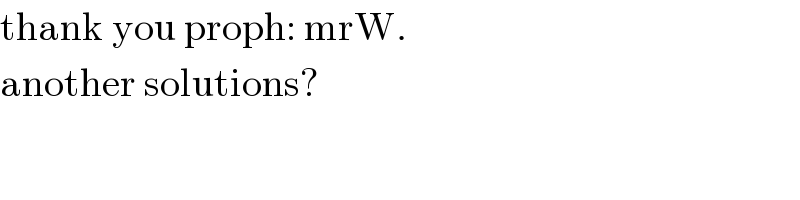
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{proph}:\:\mathrm{mrW}. \\ $$$$\mathrm{another}\:\mathrm{solutions}? \\ $$
Answered by MJS last updated on 18/Dec/19
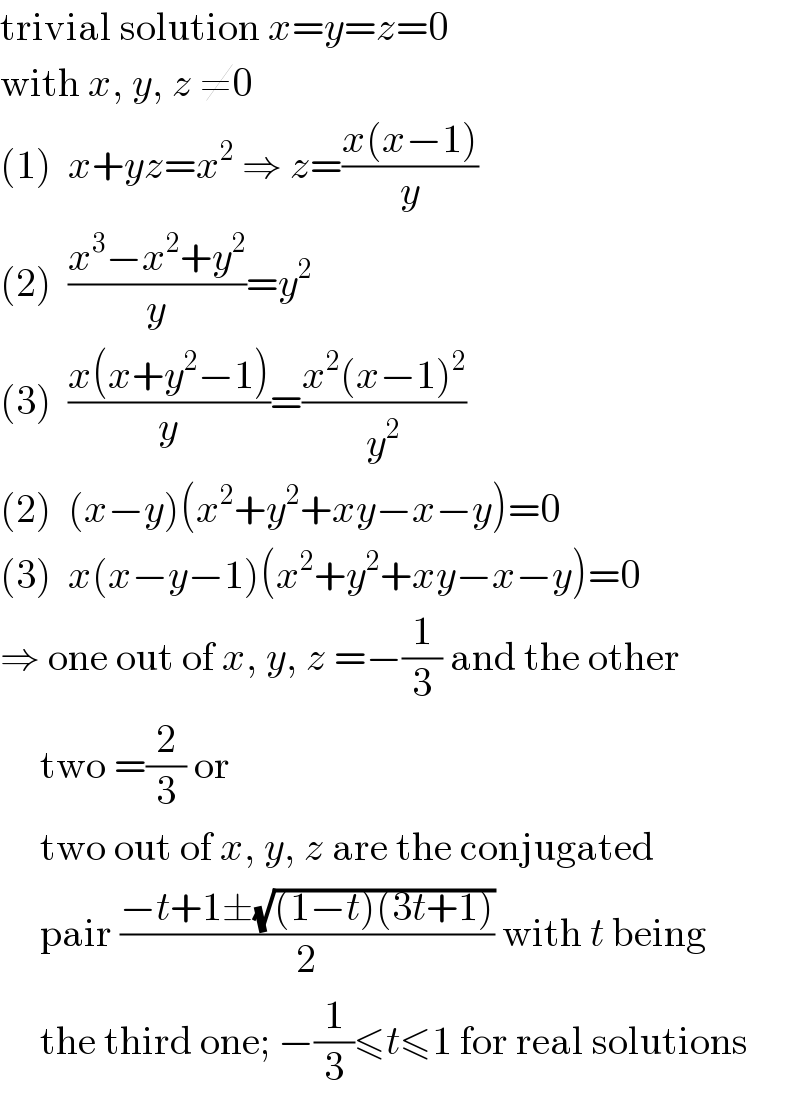
$$\mathrm{trivial}\:\mathrm{solution}\:{x}={y}={z}=\mathrm{0} \\ $$$$\mathrm{with}\:{x},\:{y},\:{z}\:\neq\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:\:{x}+{yz}={x}^{\mathrm{2}} \:\Rightarrow\:{z}=\frac{{x}\left({x}−\mathrm{1}\right)}{{y}} \\ $$$$\left(\mathrm{2}\right)\:\:\frac{{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{{y}}={y}^{\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)\:\:\frac{{x}\left({x}+{y}^{\mathrm{2}} −\mathrm{1}\right)}{{y}}=\frac{{x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} }{{y}^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}\right)\:\:\left({x}−{y}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{xy}−{x}−{y}\right)=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\:{x}\left({x}−{y}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{xy}−{x}−{y}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{one}\:\mathrm{out}\:\mathrm{of}\:{x},\:{y},\:{z}\:=−\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{and}\:\mathrm{the}\:\mathrm{other} \\ $$$$\:\:\:\:\:\mathrm{two}\:=\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{or} \\ $$$$\:\:\:\:\:\mathrm{two}\:\mathrm{out}\:\mathrm{of}\:{x},\:{y},\:{z}\:\mathrm{are}\:\mathrm{the}\:\mathrm{conjugated} \\ $$$$\:\:\:\:\:\mathrm{pair}\:\frac{−{t}+\mathrm{1}\pm\sqrt{\left(\mathrm{1}−{t}\right)\left(\mathrm{3}{t}+\mathrm{1}\right)}}{\mathrm{2}}\:\mathrm{with}\:{t}\:\mathrm{being} \\ $$$$\:\:\:\:\:\mathrm{the}\:\mathrm{third}\:\mathrm{one};\:−\frac{\mathrm{1}}{\mathrm{3}}\leqslant{t}\leqslant\mathrm{1}\:\mathrm{for}\:\mathrm{real}\:\mathrm{solutions} \\ $$
Commented by behi83417@gmail.com last updated on 18/Dec/19

$$\mathrm{thanks}\:\mathrm{in}\:\mathrm{advance}\:\mathrm{dear}\:\mathrm{proph}. \\ $$
