Question Number 75873 by Rio Michael last updated on 19/Dec/19

$$\int{xe}^{{x}} {dx} \\ $$
Answered by MJS last updated on 19/Dec/19
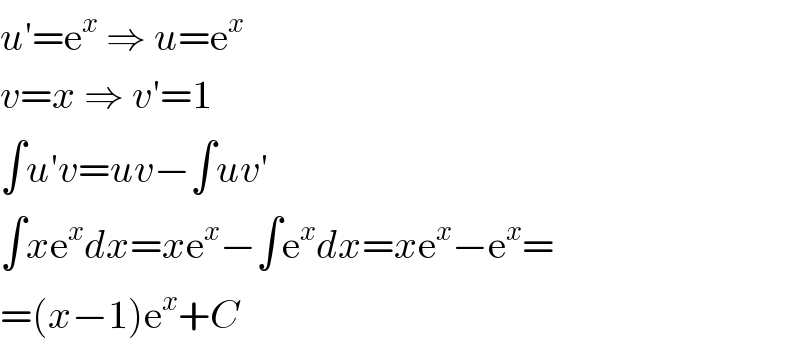
$${u}'=\mathrm{e}^{{x}} \:\Rightarrow\:{u}=\mathrm{e}^{{x}} \\ $$$${v}={x}\:\Rightarrow\:{v}'=\mathrm{1} \\ $$$$\int{u}'{v}={uv}−\int{uv}' \\ $$$$\int{x}\mathrm{e}^{{x}} {dx}={x}\mathrm{e}^{{x}} −\int\mathrm{e}^{{x}} {dx}={x}\mathrm{e}^{{x}} −\mathrm{e}^{{x}} = \\ $$$$=\left({x}−\mathrm{1}\right)\mathrm{e}^{{x}} +{C} \\ $$
Commented by Rio Michael last updated on 21/Dec/19
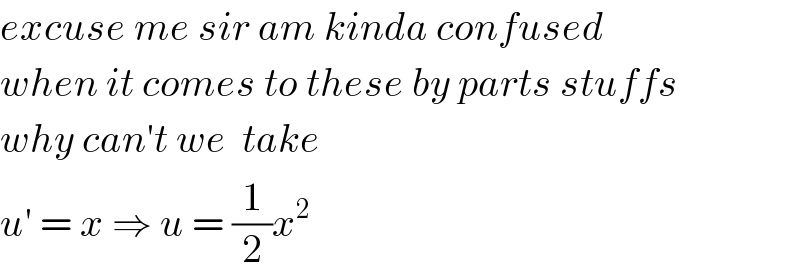
$${excuse}\:{me}\:{sir}\:{am}\:{kinda}\:{confused} \\ $$$${when}\:{it}\:{comes}\:{to}\:{these}\:{by}\:{parts}\:{stuffs} \\ $$$${why}\:{can}'{t}\:{we}\:\:{take} \\ $$$${u}'\:=\:{x}\:\Rightarrow\:{u}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \\ $$
Commented by MJS last updated on 21/Dec/19
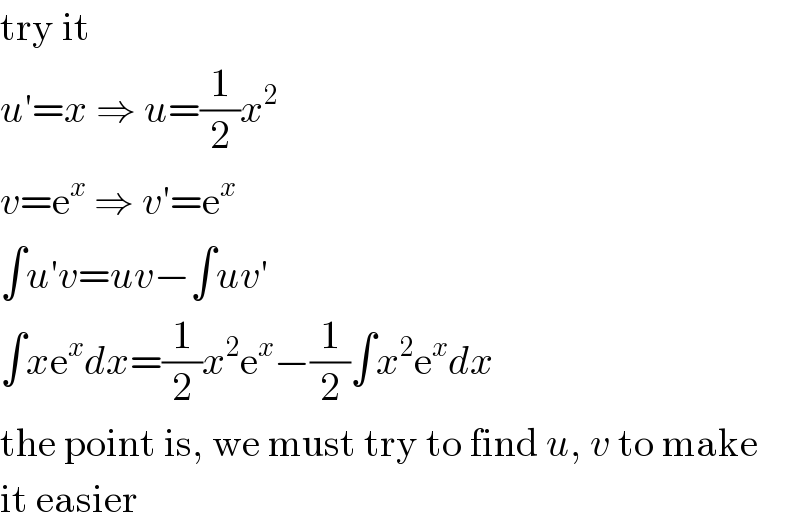
$$\mathrm{try}\:\mathrm{it} \\ $$$${u}'={x}\:\Rightarrow\:{u}=\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \\ $$$${v}=\mathrm{e}^{{x}} \:\Rightarrow\:{v}'=\mathrm{e}^{{x}} \\ $$$$\int{u}'{v}={uv}−\int{uv}' \\ $$$$\int{x}\mathrm{e}^{{x}} {dx}=\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \mathrm{e}^{{x}} −\frac{\mathrm{1}}{\mathrm{2}}\int{x}^{\mathrm{2}} \mathrm{e}^{{x}} {dx} \\ $$$$\mathrm{the}\:\mathrm{point}\:\mathrm{is},\:\mathrm{we}\:\mathrm{must}\:\mathrm{try}\:\mathrm{to}\:\mathrm{find}\:{u},\:{v}\:\mathrm{to}\:\mathrm{make} \\ $$$$\mathrm{it}\:\mathrm{easier} \\ $$
Commented by Rio Michael last updated on 21/Dec/19
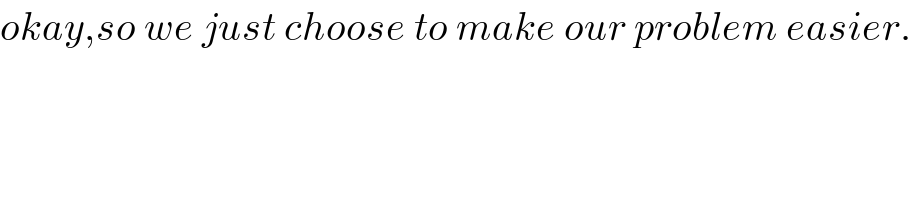
$${okay},{so}\:{we}\:{just}\:{choose}\:{to}\:{make}\:{our}\:{problem}\:{easier}. \\ $$
Commented by MJS last updated on 21/Dec/19
$$\mathrm{yes}.\:\mathrm{but}\:\mathrm{it}\:\mathrm{can}\:\mathrm{be}\:\mathrm{tricky}\:\mathrm{sometimes} \\ $$
