Menu Close

xy-24-x-3-y-xy-6-y-3-x-

Tinku Tara 0 Comments
Pin




Question Number 139874 by bramlexs22 last updated on 02/May/21
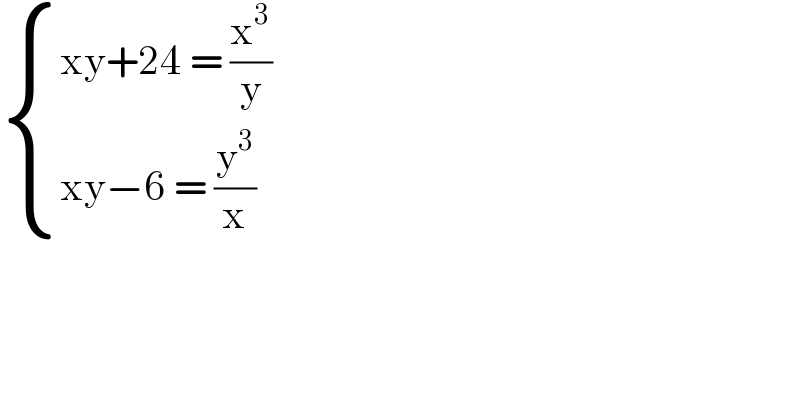
{ ((xy+24 = (x^3 /y))),((xy−6 = (y^3 /x))) :}
$$\begin{cases}{\mathrm{xy}+\mathrm{24}\:=\:\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{y}}}\\{\mathrm{xy}−\mathrm{6}\:=\:\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{x}}}\end{cases} \\ $$
Answered by EDWIN88 last updated on 03/May/21
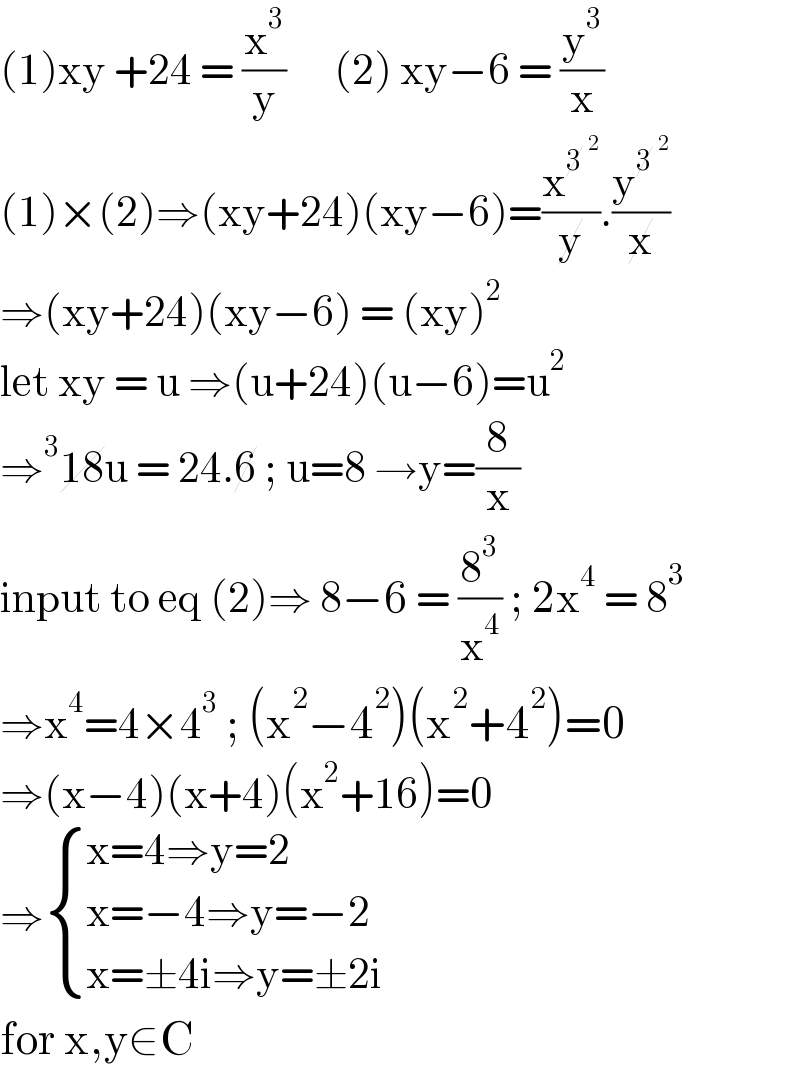
(1)xy +24 = (x^3 /y) (2) xy−6 = (y^3 /x) (1)×(2)⇒(xy+24)(xy−6)=(x^(3^2 ) /y).(y^(3^2 ) /x) ⇒(xy+24)(xy−6) = (xy)^2 let xy = u ⇒(u+24)(u−6)=u^2 ⇒^3 18u = 24.6 ; u=8 →y=(8/x) input to eq (2)⇒ 8−6 = (8^3 /x^4 ) ; 2x^4 = 8^3 ⇒x^4 =4×4^3 ; (x^2 −4^2 )(x^2 +4^2 )=0 ⇒(x−4)(x+4)(x^2 +16)=0 ⇒ { ((x=4⇒y=2)),((x=−4⇒y=−2)),((x=±4i⇒y=±2i)) :} for x,y∈C
$$\left(\mathrm{1}\right)\mathrm{xy}\:+\mathrm{24}\:=\:\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{y}}\:\:\:\:\:\:\left(\mathrm{2}\right)\:\mathrm{xy}−\mathrm{6}\:=\:\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{x}} \\ $$$$\left(\mathrm{1}\right)×\left(\mathrm{2}\right)\Rightarrow\left(\mathrm{xy}+\mathrm{24}\right)\left(\mathrm{xy}−\mathrm{6}\right)=\frac{\mathrm{x}^{\cancel{\mathrm{3}}\:^{\mathrm{2}} } }{\cancel{\mathrm{y}}}.\frac{\mathrm{y}^{\cancel{\mathrm{3}}\:^{\mathrm{2}} } }{\cancel{\mathrm{x}}} \\ $$$$\Rightarrow\left(\mathrm{xy}+\mathrm{24}\right)\left(\mathrm{xy}−\mathrm{6}\right)\:=\:\left(\mathrm{xy}\right)^{\mathrm{2}} \\ $$$$\mathrm{let}\:\mathrm{xy}\:=\:\mathrm{u}\:\Rightarrow\left(\mathrm{u}+\mathrm{24}\right)\left(\mathrm{u}−\mathrm{6}\right)=\mathrm{u}^{\mathrm{2}} \\ $$$$\Rightarrow^{\mathrm{3}} \cancel{\mathrm{18}u}\:=\:\mathrm{24}.\cancel{\mathrm{6}}\:;\:\mathrm{u}=\mathrm{8}\:\rightarrow\mathrm{y}=\frac{\mathrm{8}}{\mathrm{x}} \\ $$$$\mathrm{input}\:\mathrm{to}\:\mathrm{eq}\:\left(\mathrm{2}\right)\Rightarrow\:\mathrm{8}−\mathrm{6}\:=\:\frac{\mathrm{8}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{4}} }\:;\:\mathrm{2x}^{\mathrm{4}} \:=\:\mathrm{8}^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{4}} =\mathrm{4}×\mathrm{4}^{\mathrm{3}} \:;\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{4}\right)\left(\mathrm{x}+\mathrm{4}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{16}\right)=\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{\mathrm{x}=\mathrm{4}\Rightarrow\mathrm{y}=\mathrm{2}}\\{\mathrm{x}=−\mathrm{4}\Rightarrow\mathrm{y}=−\mathrm{2}}\\{\mathrm{x}=\pm\mathrm{4i}\Rightarrow\mathrm{y}=\pm\mathrm{2i}}\end{cases} \\ $$$$\mathrm{for}\:\mathrm{x},\mathrm{y}\in\mathrm{C} \\ $$
Answered by MJS_new last updated on 02/May/21
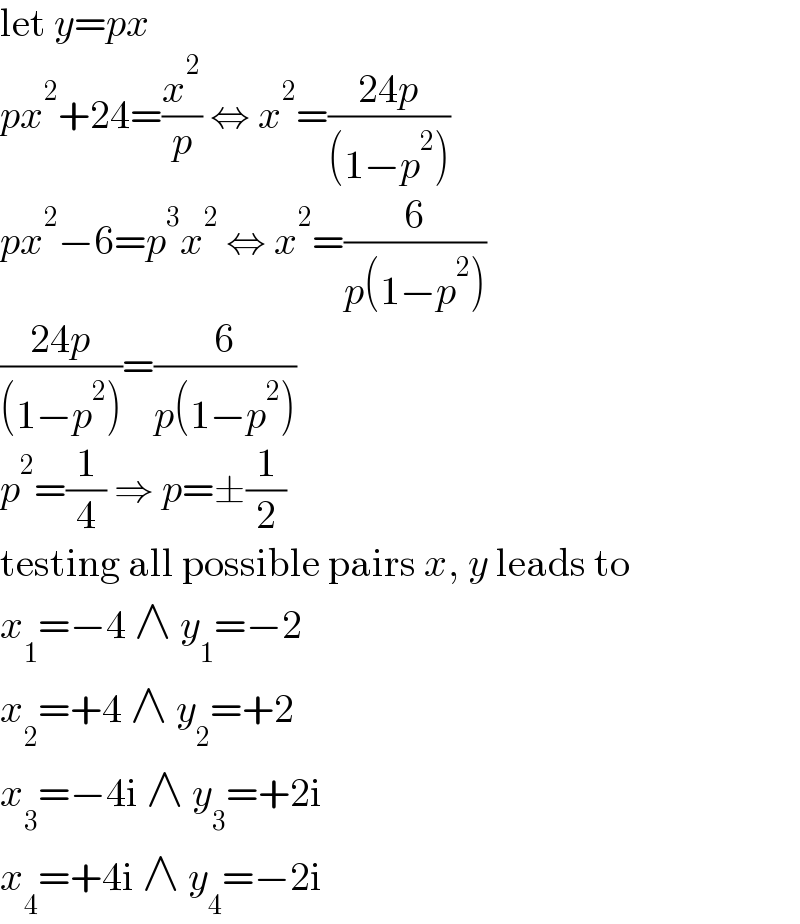
let y=px px^2 +24=(x^2 /p) ⇔ x^2 =((24p)/((1−p^2 ))) px^2 −6=p^3 x^2 ⇔ x^2 =(6/(p(1−p^2 ))) ((24p)/((1−p^2 )))=(6/(p(1−p^2 ))) p^2 =(1/4) ⇒ p=±(1/2) testing all possible pairs x, y leads to x_1 =−4 ∧ y_1 =−2 x_2 =+4 ∧ y_2 =+2 x_3 =−4i ∧ y_3 =+2i x_4 =+4i ∧ y_4 =−2i
$$\mathrm{let}\:{y}={px} \\ $$$${px}^{\mathrm{2}} +\mathrm{24}=\frac{{x}^{\mathrm{2}} }{{p}}\:\Leftrightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{24}{p}}{\left(\mathrm{1}−{p}^{\mathrm{2}} \right)} \\ $$$${px}^{\mathrm{2}} −\mathrm{6}={p}^{\mathrm{3}} {x}^{\mathrm{2}} \:\Leftrightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{6}}{{p}\left(\mathrm{1}−{p}^{\mathrm{2}} \right)} \\ $$$$\frac{\mathrm{24}{p}}{\left(\mathrm{1}−{p}^{\mathrm{2}} \right)}=\frac{\mathrm{6}}{{p}\left(\mathrm{1}−{p}^{\mathrm{2}} \right)} \\ $$$${p}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:{p}=\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{testing}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{pairs}\:{x},\:{y}\:\mathrm{leads}\:\mathrm{to} \\ $$$${x}_{\mathrm{1}} =−\mathrm{4}\:\wedge\:{y}_{\mathrm{1}} =−\mathrm{2} \\ $$$${x}_{\mathrm{2}} =+\mathrm{4}\:\wedge\:{y}_{\mathrm{2}} =+\mathrm{2} \\ $$$${x}_{\mathrm{3}} =−\mathrm{4i}\:\wedge\:{y}_{\mathrm{3}} =+\mathrm{2i} \\ $$$${x}_{\mathrm{4}} =+\mathrm{4i}\:\wedge\:{y}_{\mathrm{4}} =−\mathrm{2i} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *