y-2-x-2-5-y-x-2-Find-x-y-

Question Number 137982 by mey3nipaba last updated on 08/Apr/21

y^{2} - x^{2} = 5 {(y - x)}^{2} . F i n d x : y

Commented by mey3nipaba last updated on 08/Apr/21

p l e a s e h e l p

Answered by Dwaipayan Shikari last updated on 08/Apr/21

\frac{y^{2} - x^{2}}{{(y - x)}^{2}} = 5 \Rightarrow \frac{(y - x) (y + x)}{(y - x) (y - x)} = 5

\Rightarrow \frac{y + x}{y - x} = 5 \Rightarrow \frac{y + x + (y - x)}{y + x - (y - x)} = \frac{5 + 1}{5 - 1} \Rightarrow \frac{y}{x} = \frac{6}{4}

\Rightarrow \frac{x}{y} = \frac{2}{3}

Commented by mey3nipaba last updated on 08/Apr/21

t h a n k s s o m u c h . i h a d t h e a n s w e r b u t w a n t e d t o c o n f i r m

Answered by Rasheed.Sindhi last updated on 08/Apr/21

A n A l t e r n a t e W a y

\frac{x}{y} = k \Rightarrow x = y k

y^{2} - x^{2} = 5 {(y - x)}^{2}

\Rightarrow y^{2} - {(y k)}^{2} = 5 {(y - y k)}^{2}

y^{2} (1 - k^{2}) = 5 y^{2} {(1 - k)}^{2}

y^{2} (1 - k) (1 + k) - 5 y^{2} {(1 - k)}^{2} = 0

(1 - k) (y^{2} (1 + k) - 5 y^{2} (1 - k)) = 0

k = 1 ∣ y^{2} (1 + k) = 5 y^{2} (1 - k)

x : y = 1 : 1 ∣ \frac{1 + k}{1 - k} = \frac{5 y^{2}}{y^{2}} = 5

∣ 1 + k = 5 - 5 k

∣ 6 k = 4 \Rightarrow k = 2 / 3

∣ x : y = 2 : 3

Answered by nadovic last updated on 08/Apr/21

y^{2} - x^{2} = 5 y^{2} - 10 x y + 5 x^{2}

6 x^{2} - 10 x y + 4 y^{2} = 0

2 (3 x^{2} - 5 x y + 2 y^{2}) = 0

2 (x - y) (3 x - 2 y) = 0

\frac{x}{y} = 1 o r \frac{x}{y} = \frac{2}{3}

x : y = 1 : 1 o r x : y = 2 : 3

Answered by Rasheed.Sindhi last updated on 09/Apr/21

y^{2} - x^{2} = 5 {(y - x)}^{2} . F i n d x : y

y^{2} (1 - \frac{x^{2}}{y^{2}}) = 5 y^{2} {(1 - \frac{x}{y})}^{2}

y \neq 0 \Rightarrow (1 - \frac{x^{2}}{y^{2}}) = 5 {(1 - \frac{x}{y})}^{2}

\frac{x}{y} = u \Rightarrow (1 - u^{2}) = 5 {(1 - u)}^{2}

(1 - u) (1 + u) - 5 {(1 - u)}^{2} = 0

(1 - u) (1 + u - 5 + 5 u) = 0

(1 - u) (6 u - 4) = 0

u = 1 ∣ u = \frac{2}{3}

x : y = 1 : 1 ∣ x : y = 2 : 3

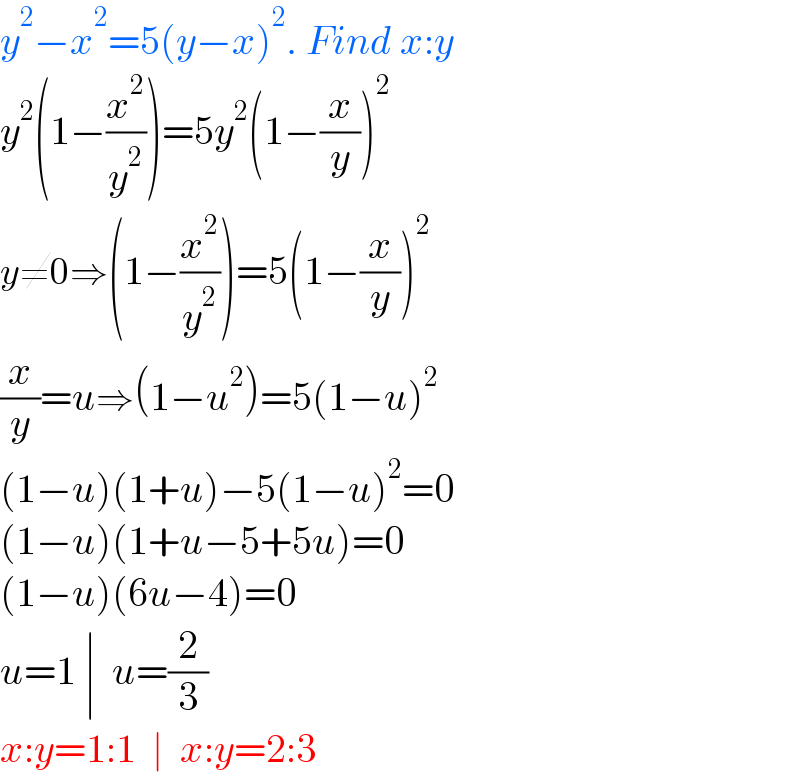
Answered by MJS_new last updated on 09/Apr/21

(y - x) (y + x) = 5 {(y - x)}^{2}

(1) y - x = 0 \Rightarrow \frac{x}{y} = 1

(2) y + x = 5 (y - x) \Rightarrow \frac{x}{y} = \frac{2}{3}

Facebook Tweet Pin