y-2xy-

Question Number 143878 by akmalovna05 last updated on 19/Jun/21

$$\mathrm{y}'''=\mathrm{2xy}'' \\ $$

Answered by Ar Brandon last updated on 19/Jun/21

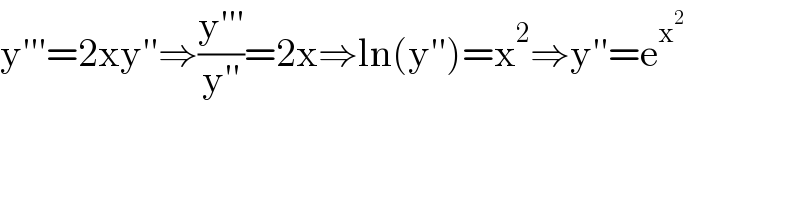
y′′′=2xy′′⇒((y′′′)/(y′′))=2x⇒ln(y′′)=x^2 ⇒y′′=e^x^2

$$\mathrm{y}'''=\mathrm{2xy}''\Rightarrow\frac{\mathrm{y}'''}{\mathrm{y}''}=\mathrm{2x}\Rightarrow\mathrm{ln}\left(\mathrm{y}''\right)=\mathrm{x}^{\mathrm{2}} \Rightarrow\mathrm{y}''=\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \\ $$

Answered by ajfour last updated on 19/Jun/21

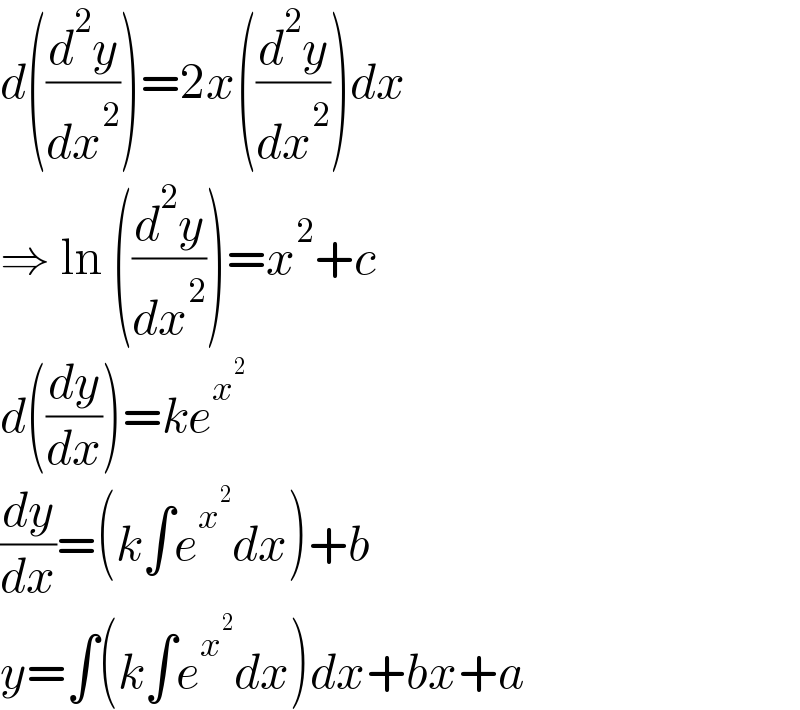
d((d^2 y/dx^2 ))=2x((d^2 y/dx^2 ))dx ⇒ ln ((d^2 y/dx^2 ))=x^2 +c d((dy/dx))=ke^x^2 (dy/dx)=(k∫e^x^2 dx)+b y=∫(k∫e^x^2 dx)dx+bx+a

$${d}\left(\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right)=\mathrm{2}{x}\left(\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right){dx} \\ $$$$\Rightarrow\:\mathrm{ln}\:\left(\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right)={x}^{\mathrm{2}} +{c} \\ $$$${d}\left(\frac{{dy}}{{dx}}\right)={ke}^{{x}^{\mathrm{2}} } \\ $$$$\frac{{dy}}{{dx}}=\left({k}\int{e}^{{x}^{\mathrm{2}} } {dx}\right)+{b} \\ $$$${y}=\int\left({k}\int{e}^{{x}^{\mathrm{2}} } {dx}\right){dx}+{bx}+{a} \\ $$

Answered by Olaf_Thorendsen last updated on 19/Jun/21

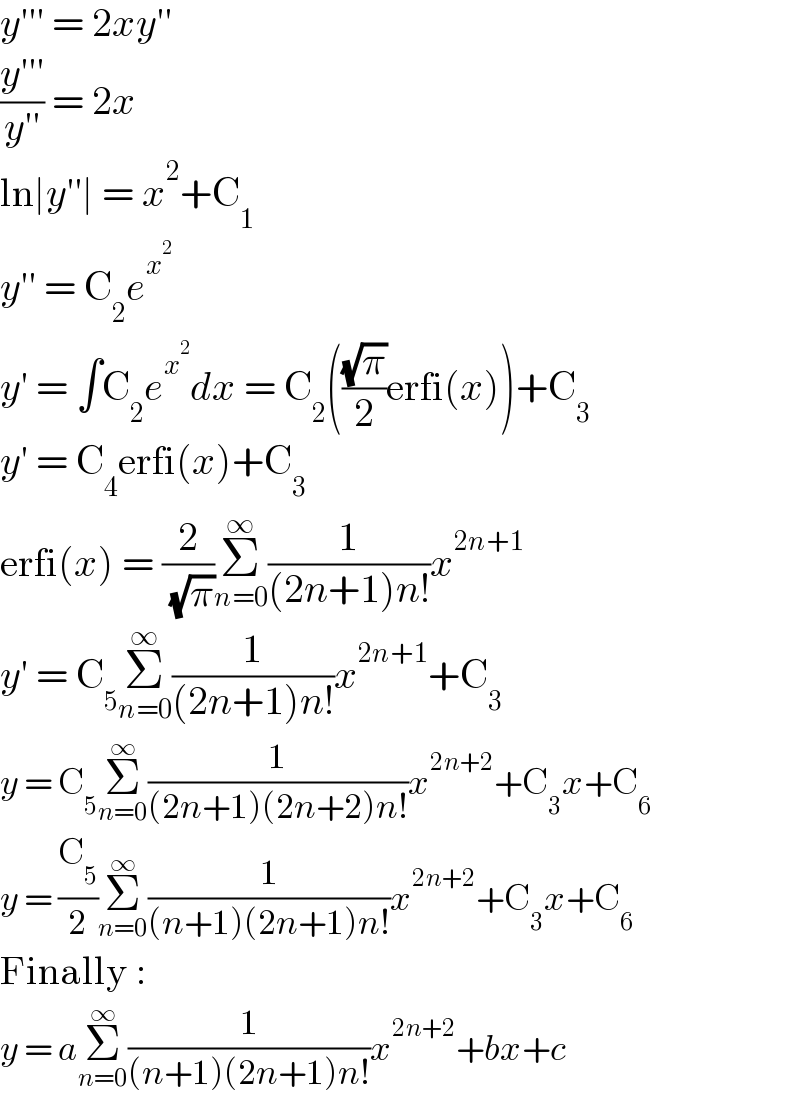
y′′′ = 2xy′′ ((y′′′)/(y′′)) = 2x ln∣y′′∣ = x^2 +C_1 y′′ = C_2 e^x^2 y′ = ∫C_2 e^x^2 dx = C_2 (((√π)/2)erfi(x))+C_3 y′ = C_4 erfi(x)+C_3 erfi(x) = (2/( (√π)))Σ_(n=0) ^∞ (1/((2n+1)n!))x^(2n+1) y′ = C_5 Σ_(n=0) ^∞ (1/((2n+1)n!))x^(2n+1) +C_3 y = C_5 Σ_(n=0) ^∞ (1/((2n+1)(2n+2)n!))x^(2n+2) +C_3 x+C_6 y = (C_5 /2)Σ_(n=0) ^∞ (1/((n+1)(2n+1)n!))x^(2n+2) +C_3 x+C_6 Finally : y = aΣ_(n=0) ^∞ (1/((n+1)(2n+1)n!))x^(2n+2) +bx+c

$${y}'''\:=\:\mathrm{2}{xy}'' \\ $$$$\frac{{y}'''}{{y}''}\:=\:\mathrm{2}{x} \\ $$$$\mathrm{ln}\mid{y}''\mid\:=\:{x}^{\mathrm{2}} +\mathrm{C}_{\mathrm{1}} \\ $$$${y}''\:=\:\mathrm{C}_{\mathrm{2}} {e}^{{x}^{\mathrm{2}} } \\ $$$${y}'\:=\:\int\mathrm{C}_{\mathrm{2}} {e}^{{x}^{\mathrm{2}} } {dx}\:=\:\mathrm{C}_{\mathrm{2}} \left(\frac{\sqrt{\pi}}{\mathrm{2}}\mathrm{erfi}\left({x}\right)\right)+\mathrm{C}_{\mathrm{3}} \\ $$$${y}'\:=\:\mathrm{C}_{\mathrm{4}} \mathrm{erfi}\left({x}\right)+\mathrm{C}_{\mathrm{3}} \\ $$$$\mathrm{erfi}\left({x}\right)\:=\:\frac{\mathrm{2}}{\:\sqrt{\pi}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}{x}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$${y}'\:=\:\mathrm{C}_{\mathrm{5}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}{x}^{\mathrm{2}{n}+\mathrm{1}} +\mathrm{C}_{\mathrm{3}} \\ $$$${y}\:=\:\mathrm{C}_{\mathrm{5}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{2}\right){n}!}{x}^{\mathrm{2}{n}+\mathrm{2}} +\mathrm{C}_{\mathrm{3}} {x}+\mathrm{C}_{\mathrm{6}} \\ $$$${y}\:=\:\frac{\mathrm{C}_{\mathrm{5}} }{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}{x}^{\mathrm{2}{n}+\mathrm{2}} +\mathrm{C}_{\mathrm{3}} {x}+\mathrm{C}_{\mathrm{6}} \\ $$$$\mathrm{Finally}\:: \\ $$$${y}\:=\:{a}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}{x}^{\mathrm{2}{n}+\mathrm{2}} +{bx}+{c} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply