Question Number 141849 by iloveisrael last updated on 24/May/21
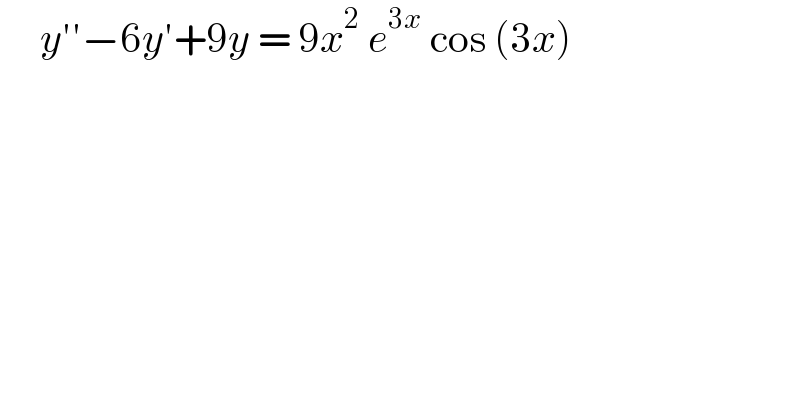
$$\:\:\:\:\:{y}''−\mathrm{6}{y}'+\mathrm{9}{y}\:=\:\mathrm{9}{x}^{\mathrm{2}} \:{e}^{\mathrm{3}{x}} \:\mathrm{cos}\:\left(\mathrm{3}{x}\right)\:\: \\ $$
Answered by qaz last updated on 24/May/21
![y′′−6y′+9y=9x^2 e^(3x) cos (3x) y_p =(1/(D^2 −6D+9))9x^2 e^(3x) cos (3x) =9(1/((D−3)^2 ))x^2 e^(3x) cos (3x) =9e^(3x) ℜ(1/D^2 )x^2 e^(3ix) =9e^(3x) ℜe^(3ix) (1/((D+3i)^2 ))x^2 =9e^(3x) ℜe^(3ix) (1/(D^2 +6iD−9))x^2 =−9e^(3x) ℜe^(3ix) (1/(9[1−((D^2 /9)+((2iD)/3))]))x^2 =−e^(3x) ℜe^(3ix) [1+((D^2 /9)+((2iD)/3))+((D^2 /9)+((2iD)/3))^2 +...]x^2 =−e^(3x) ℜe^(3ix) (x^2 +((4i)/3)x−(2/3)) =−e^(3x) [x^2 cos (3x)−(4/3)xsin (3x)−(2/3)cos (3x)] ⇒y=e^(3x) (C_1 +C_2 x)−e^(3x) [x^2 cos (3x)−(4/3)xsin (3x)−(2/3)cos (3x)] =e^(3x) [C_1 +C_2 x−x^2 cos (3x)+(4/3)xsin (3x)+(2/3)cos (3x)]](https://www.tinkutara.com/question/Q141852.png)
$${y}''−\mathrm{6}{y}'+\mathrm{9}{y}=\mathrm{9}{x}^{\mathrm{2}} {e}^{\mathrm{3}{x}} \mathrm{cos}\:\left(\mathrm{3}{x}\right) \\ $$$${y}_{{p}} =\frac{\mathrm{1}}{{D}^{\mathrm{2}} −\mathrm{6}{D}+\mathrm{9}}\mathrm{9}{x}^{\mathrm{2}} {e}^{\mathrm{3}{x}} \mathrm{cos}\:\left(\mathrm{3}{x}\right) \\ $$$$=\mathrm{9}\frac{\mathrm{1}}{\left({D}−\mathrm{3}\right)^{\mathrm{2}} }{x}^{\mathrm{2}} {e}^{\mathrm{3}{x}} \mathrm{cos}\:\left(\mathrm{3}{x}\right) \\ $$$$=\mathrm{9}{e}^{\mathrm{3}{x}} \Re\frac{\mathrm{1}}{{D}^{\mathrm{2}} }{x}^{\mathrm{2}} {e}^{\mathrm{3}{ix}} \\ $$$$=\mathrm{9}{e}^{\mathrm{3}{x}} \Re{e}^{\mathrm{3}{ix}} \frac{\mathrm{1}}{\left({D}+\mathrm{3}{i}\right)^{\mathrm{2}} }{x}^{\mathrm{2}} \\ $$$$=\mathrm{9}{e}^{\mathrm{3}{x}} \Re{e}^{\mathrm{3}{ix}} \frac{\mathrm{1}}{{D}^{\mathrm{2}} +\mathrm{6}{iD}−\mathrm{9}}{x}^{\mathrm{2}} \\ $$$$=−\mathrm{9}{e}^{\mathrm{3}{x}} \Re{e}^{\mathrm{3}{ix}} \frac{\mathrm{1}}{\mathrm{9}\left[\mathrm{1}−\left(\frac{{D}^{\mathrm{2}} }{\mathrm{9}}+\frac{\mathrm{2}{iD}}{\mathrm{3}}\right)\right]}{x}^{\mathrm{2}} \\ $$$$=−{e}^{\mathrm{3}{x}} \Re{e}^{\mathrm{3}{ix}} \left[\mathrm{1}+\left(\frac{{D}^{\mathrm{2}} }{\mathrm{9}}+\frac{\mathrm{2}{iD}}{\mathrm{3}}\right)+\left(\frac{{D}^{\mathrm{2}} }{\mathrm{9}}+\frac{\mathrm{2}{iD}}{\mathrm{3}}\right)^{\mathrm{2}} +…\right]{x}^{\mathrm{2}} \\ $$$$=−{e}^{\mathrm{3}{x}} \Re{e}^{\mathrm{3}{ix}} \left({x}^{\mathrm{2}} +\frac{\mathrm{4}{i}}{\mathrm{3}}{x}−\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$$=−{e}^{\mathrm{3}{x}} \left[{x}^{\mathrm{2}} \mathrm{cos}\:\left(\mathrm{3}{x}\right)−\frac{\mathrm{4}}{\mathrm{3}}{x}\mathrm{sin}\:\left(\mathrm{3}{x}\right)−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{cos}\:\left(\mathrm{3}{x}\right)\right] \\ $$$$\Rightarrow{y}={e}^{\mathrm{3}{x}} \left({C}_{\mathrm{1}} +{C}_{\mathrm{2}} {x}\right)−{e}^{\mathrm{3}{x}} \left[{x}^{\mathrm{2}} \mathrm{cos}\:\left(\mathrm{3}{x}\right)−\frac{\mathrm{4}}{\mathrm{3}}{x}\mathrm{sin}\:\left(\mathrm{3}{x}\right)−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{cos}\:\left(\mathrm{3}{x}\right)\right] \\ $$$$\:\:\:\:\:\:\:={e}^{\mathrm{3}{x}} \left[{C}_{\mathrm{1}} +{C}_{\mathrm{2}} {x}−{x}^{\mathrm{2}} \mathrm{cos}\:\left(\mathrm{3}{x}\right)+\frac{\mathrm{4}}{\mathrm{3}}{x}\mathrm{sin}\:\left(\mathrm{3}{x}\right)+\frac{\mathrm{2}}{\mathrm{3}}\mathrm{cos}\:\left(\mathrm{3}{x}\right)\right] \\ $$
