Question Number 133631 by liberty last updated on 23/Feb/21
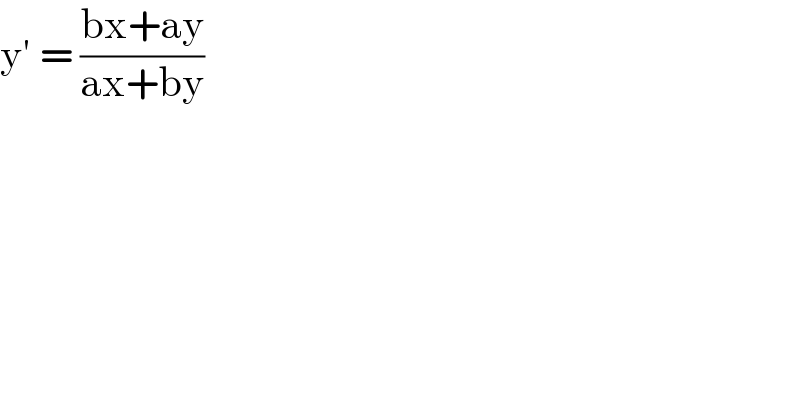
$$\mathrm{y}'\:=\:\frac{\mathrm{bx}+\mathrm{ay}}{\mathrm{ax}+\mathrm{by}} \\ $$
Answered by TheSupreme last updated on 23/Feb/21
![caso 1: b=0 y′=((ay)/(ax))=(y/x) ln(y)=ln(x)+c y=c_1 x caso 2: b≠0 ξ=(a/b) y′=((x+ξy)/(ξx+y)) ξx+y=u y′=u′+ξ u′+ξ=((x+ξ(u+ξx))/u) u′+ξ=(1/u)(x+ξu+ξ^2 x) uu′+ξu=x+ξu+ξ^2 x uu′=x(1+ξ^2 ) (u^2 /2)=(x^2 /2)(1+ξ^2 )+c u^2 =x^2 (1+ξ^2 )+c u=∣x∣(√(c+1+ξ^2 )) y=∣x∣(√(c+1+ξ^2 ))+ξx+c verify for c=0 y′=sgn(x)(√(1+ξ^2 ))+ξ sgn(x)(√(1+ξ^2 ))+ξ=((x+ξ∣x∣(√(1+ξ^2 ))+ξ^2 x)/(∣x∣(√(1+ξ^2 )))) =((x[(1+ξ^2 )+ξsgn(x)(√(1+ξ^2 ))])/(∣x∣(√(1+ξ^2 ))))=sgn(x)(√(1+ξ^2 ))+ξ](https://www.tinkutara.com/question/Q133632.png)
$${caso}\:\mathrm{1}:\:{b}=\mathrm{0}\: \\ $$$${y}'=\frac{{ay}}{{ax}}=\frac{{y}}{{x}} \\ $$$${ln}\left({y}\right)={ln}\left({x}\right)+{c} \\ $$$${y}={c}_{\mathrm{1}} {x} \\ $$$${caso}\:\mathrm{2}:\:{b}\neq\mathrm{0} \\ $$$$\xi=\frac{{a}}{{b}} \\ $$$${y}'=\frac{{x}+\xi{y}}{\xi{x}+{y}} \\ $$$$\xi{x}+{y}={u} \\ $$$${y}'={u}'+\xi \\ $$$${u}'+\xi=\frac{{x}+\xi\left({u}+\xi{x}\right)}{{u}} \\ $$$${u}'+\xi=\frac{\mathrm{1}}{{u}}\left({x}+\xi{u}+\xi^{\mathrm{2}} {x}\right) \\ $$$${uu}'+\xi{u}={x}+\xi{u}+\xi^{\mathrm{2}} {x} \\ $$$${uu}'={x}\left(\mathrm{1}+\xi^{\mathrm{2}} \right) \\ $$$$\frac{{u}^{\mathrm{2}} }{\mathrm{2}}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{1}+\xi^{\mathrm{2}} \right)+{c} \\ $$$${u}^{\mathrm{2}} ={x}^{\mathrm{2}} \left(\mathrm{1}+\xi^{\mathrm{2}} \right)+{c} \\ $$$$ \\ $$$${u}=\mid{x}\mid\sqrt{{c}+\mathrm{1}+\xi^{\mathrm{2}} } \\ $$$${y}=\mid{x}\mid\sqrt{{c}+\mathrm{1}+\xi^{\mathrm{2}} }+\xi{x}+{c} \\ $$$$ \\ $$$${verify}\:{for}\:{c}=\mathrm{0} \\ $$$${y}'={sgn}\left({x}\right)\sqrt{\mathrm{1}+\xi^{\mathrm{2}} }+\xi \\ $$$${sgn}\left({x}\right)\sqrt{\mathrm{1}+\xi^{\mathrm{2}} }+\xi=\frac{{x}+\xi\mid{x}\mid\sqrt{\mathrm{1}+\xi^{\mathrm{2}} }+\xi^{\mathrm{2}} {x}}{\mid{x}\mid\sqrt{\mathrm{1}+\xi^{\mathrm{2}} }} \\ $$$$=\frac{{x}\left[\left(\mathrm{1}+\xi^{\mathrm{2}} \right)+\xi{sgn}\left({x}\right)\sqrt{\mathrm{1}+\xi^{\mathrm{2}} }\right]}{\mid{x}\mid\sqrt{\mathrm{1}+\xi^{\mathrm{2}} }}={sgn}\left({x}\right)\sqrt{\mathrm{1}+\xi^{\mathrm{2}} }+\xi \\ $$$$ \\ $$$$ \\ $$
Answered by mr W last updated on 23/Feb/21
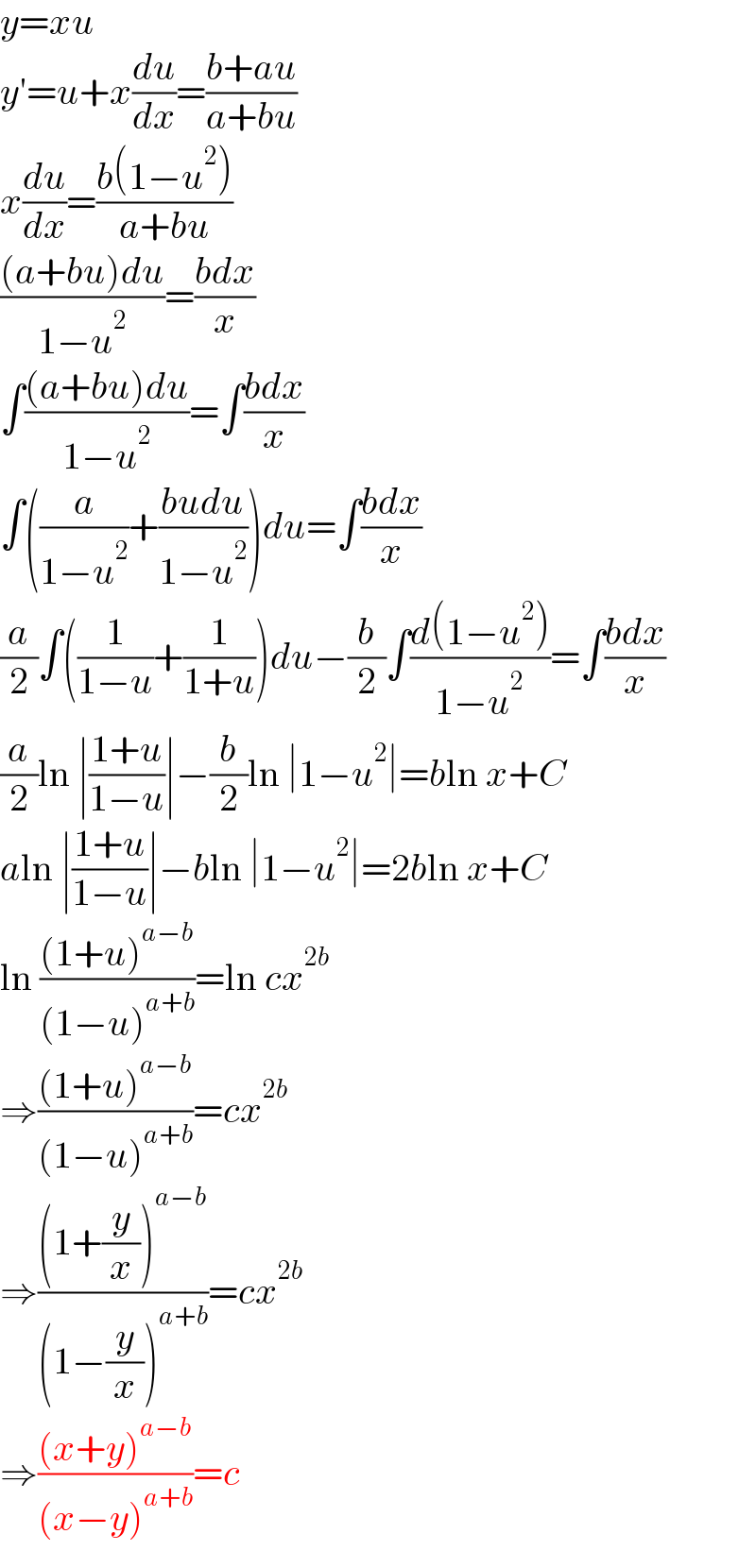
$${y}={xu} \\ $$$${y}'={u}+{x}\frac{{du}}{{dx}}=\frac{{b}+{au}}{{a}+{bu}} \\ $$$${x}\frac{{du}}{{dx}}=\frac{{b}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}{{a}+{bu}} \\ $$$$\frac{\left({a}+{bu}\right){du}}{\mathrm{1}−{u}^{\mathrm{2}} }=\frac{{bdx}}{{x}} \\ $$$$\int\frac{\left({a}+{bu}\right){du}}{\mathrm{1}−{u}^{\mathrm{2}} }=\int\frac{{bdx}}{{x}} \\ $$$$\int\left(\frac{{a}}{\mathrm{1}−{u}^{\mathrm{2}} }+\frac{{budu}}{\mathrm{1}−{u}^{\mathrm{2}} }\right){du}=\int\frac{{bdx}}{{x}} \\ $$$$\frac{{a}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\mathrm{1}−{u}}+\frac{\mathrm{1}}{\mathrm{1}+{u}}\right){du}−\frac{{b}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}{\mathrm{1}−{u}^{\mathrm{2}} }=\int\frac{{bdx}}{{x}} \\ $$$$\frac{{a}}{\mathrm{2}}\mathrm{ln}\:\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid−\frac{{b}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{1}−{u}^{\mathrm{2}} \mid={b}\mathrm{ln}\:{x}+{C} \\ $$$${a}\mathrm{ln}\:\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid−{b}\mathrm{ln}\:\mid\mathrm{1}−{u}^{\mathrm{2}} \mid=\mathrm{2}{b}\mathrm{ln}\:{x}+{C} \\ $$$$\mathrm{ln}\:\frac{\left(\mathrm{1}+{u}\right)^{{a}−{b}} }{\left(\mathrm{1}−{u}\right)^{{a}+{b}} }=\mathrm{ln}\:{cx}^{\mathrm{2}{b}} \\ $$$$\Rightarrow\frac{\left(\mathrm{1}+{u}\right)^{{a}−{b}} }{\left(\mathrm{1}−{u}\right)^{{a}+{b}} }={cx}^{\mathrm{2}{b}} \\ $$$$\Rightarrow\frac{\left(\mathrm{1}+\frac{{y}}{{x}}\right)^{{a}−{b}} }{\left(\mathrm{1}−\frac{{y}}{{x}}\right)^{{a}+{b}} }={cx}^{\mathrm{2}{b}} \\ $$$$\Rightarrow\frac{\left({x}+{y}\right)^{{a}−{b}} }{\left({x}−{y}\right)^{{a}+{b}} }={c} \\ $$
Answered by bobhans last updated on 23/Feb/21
![let y = ux ⇒(dy/dx) = u + x (du/dx) ⇔u+x (du/dx) = ((bx+aux)/(ax+bux))=((b+au)/(a+bu)) ⇔ x (du/dx) = ((b+au−au−bu^2 )/(a+bu)) ⇔ x (du/dx) = ((b−bu^2 )/(a+bu)) ⇒ ((a+bu)/(b(1−u^2 ))) du = (dx/x) Partial fraction ((a+bu)/(1−u^2 )) = (p/(1+u)) + (q/(1−u)) p = [((a+bu)/(1−u)) ]_(u=−1) = ((b−a)/2) q= [ ((a+bu)/(1+u)) ]_(u=1) = ((b+a)/2) ⇒(1/b)∫(((b−a)/(2(1+u))) + ((b+a)/(2(1−u))))du=∫ (dx/x) ((b−a)/2) ln ∣1+u∣−((b+a)/2) ln ∣1+u∣= b ln ∣Cx∣ (b−a)ln ∣((y+x)/x)∣ −(b+a)ln ∣((y−x)/x)∣=2b ln ∣Cx∣](https://www.tinkutara.com/question/Q133638.png)
$${let}\:{y}\:=\:{ux}\:\Rightarrow\frac{{dy}}{{dx}}\:=\:{u}\:+\:{x}\:\frac{{du}}{{dx}} \\ $$$$\Leftrightarrow{u}+{x}\:\frac{{du}}{{dx}}\:=\:\frac{{bx}+{aux}}{{ax}+{bux}}=\frac{{b}+{au}}{{a}+{bu}} \\ $$$$\Leftrightarrow\:{x}\:\frac{{du}}{{dx}}\:=\:\frac{{b}+{au}−{au}−{bu}^{\mathrm{2}} }{{a}+{bu}} \\ $$$$\Leftrightarrow\:{x}\:\frac{{du}}{{dx}}\:=\:\frac{{b}−{bu}^{\mathrm{2}} }{{a}+{bu}} \\ $$$$\Rightarrow\:\frac{{a}+{bu}}{{b}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}\:{du}\:=\:\frac{{dx}}{{x}} \\ $$$${Partial}\:{fraction}\: \\ $$$$\:\frac{{a}+{bu}}{\mathrm{1}−{u}^{\mathrm{2}} }\:=\:\frac{{p}}{\mathrm{1}+{u}}\:+\:\frac{{q}}{\mathrm{1}−{u}} \\ $$$${p}\:=\:\left[\frac{{a}+{bu}}{\mathrm{1}−{u}}\:\right]_{{u}=−\mathrm{1}} =\:\frac{{b}−{a}}{\mathrm{2}} \\ $$$${q}=\:\left[\:\frac{{a}+{bu}}{\mathrm{1}+{u}}\:\right]_{{u}=\mathrm{1}} =\:\frac{{b}+{a}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{b}}\int\left(\frac{{b}−{a}}{\mathrm{2}\left(\mathrm{1}+{u}\right)}\:+\:\frac{{b}+{a}}{\mathrm{2}\left(\mathrm{1}−{u}\right)}\right){du}=\int\:\frac{{dx}}{{x}} \\ $$$$\:\frac{{b}−{a}}{\mathrm{2}}\:\mathrm{ln}\:\mid\mathrm{1}+{u}\mid−\frac{{b}+{a}}{\mathrm{2}}\:\mathrm{ln}\:\mid\mathrm{1}+{u}\mid=\:{b}\:\mathrm{ln}\:\mid{Cx}\mid \\ $$$$\left({b}−{a}\right)\mathrm{ln}\:\mid\frac{{y}+{x}}{{x}}\mid\:−\left({b}+{a}\right)\mathrm{ln}\:\mid\frac{{y}−{x}}{{x}}\mid=\mathrm{2}{b}\:\mathrm{ln}\:\mid{Cx}\mid \\ $$
