y-e-y-pls-solve-

Question Number 73080 by oyemi kemewari last updated on 06/Nov/19

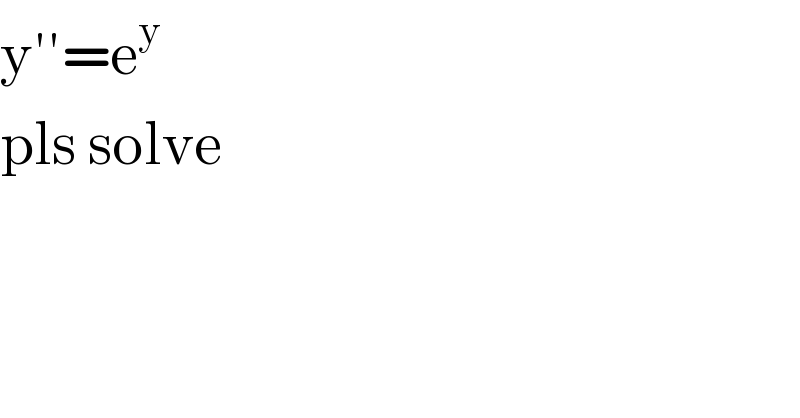
$$\mathrm{y}''=\mathrm{e}^{\mathrm{y}} \\ $$$$\mathrm{pls}\:\mathrm{solve} \\ $$

Answered by mind is power last updated on 06/Nov/19

y′′.y′=y′e^y ⇒(y′)^2 =2e^y +c ⇒y′ { ((√(2e^y +c))),((−(√(2e^y +c)))) :} y′=(√(2e^y +c)) ⇔(dy/( (√(2e^y +c))))=dx ⇔∫((e^(−(y/2)) dy)/( (√2)(√(1+(c/2)e^(−y) ))))=x+b ∫(dx/( (√(1+x^2 ))))=argsh(x) if c≥0 (√(c/2))e^(−(y/2)) =w⇒dw=−(1/2)w ∫(1/(−2(√c))).(dw/( (√(1+w^2 ))))=−(1/(2(√c)))argsh(w)=−((argsh(((√c)/( (√2)))e^(−(y/2)) ))/(2(√c))) if c≤0 ∫(dx/( (√(1−x^2 ))))=arcsin(x) ⇒∫(e^(−(y/2)) /( (√2)(√(1+(c/2)e^(−y) )))) w=(√(−(c/2)))e^(−(y/2)) ∫(dw/(−2(√(−c))((√(1−w^2 )))))=−((arcsin(w))/(2(√(−c))))=−((arcsin((√((−c)/2))e^((−y)/2) ))/(2(√(−c)))) c≥0⇒−((argsh((√(c/2)).e^((−y)/2) ))/(2(√c)))=x+b ⇒argsh((√(c/2))e^((−y)/2) )=−2(√c)(x+b) ⇒y=−2ln{(√(2/c)).sh(−2(√c)(x+b))} −2(√c)(x+b)≥0⇒x≥−b c≤0 y=−2ln{(2/( (√(−c))))(sin(−2(√(−c))(x+b)).} 2kπ<−2(√(−c))(x+b)<(2k+1)π because ln(x) is defind in x>0 ⇒ x∈]((2k+1)/(−2(√(−c))))π_ −b,((2kπ)/(−2(√(−c))))−b[ for a given integer k

$$\mathrm{y}''.\mathrm{y}'=\mathrm{y}'\mathrm{e}^{\mathrm{y}} \\ $$$$\Rightarrow\left(\mathrm{y}'\right)^{\mathrm{2}} =\mathrm{2e}^{\mathrm{y}} +\mathrm{c} \\ $$$$\Rightarrow\mathrm{y}'\begin{cases}{\sqrt{\mathrm{2e}^{\mathrm{y}} +\mathrm{c}}}\\{−\sqrt{\mathrm{2e}^{\mathrm{y}} +\mathrm{c}}}\end{cases} \\ $$$$\mathrm{y}'=\sqrt{\mathrm{2e}^{\mathrm{y}} +\mathrm{c}} \\ $$$$\Leftrightarrow\frac{\mathrm{dy}}{\:\sqrt{\mathrm{2e}^{\mathrm{y}} +\mathrm{c}}}=\mathrm{dx} \\ $$$$\Leftrightarrow\int\frac{\mathrm{e}^{−\frac{\mathrm{y}}{\mathrm{2}}} \mathrm{dy}}{\:\sqrt{\mathrm{2}}\sqrt{\mathrm{1}+\frac{\mathrm{c}}{\mathrm{2}}\mathrm{e}^{−\mathrm{y}} }}=\mathrm{x}+\mathrm{b} \\ $$$$\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}=\mathrm{argsh}\left(\mathrm{x}\right) \\ $$$$\mathrm{if}\:\mathrm{c}\geqslant\mathrm{0} \\ $$$$\sqrt{\frac{\mathrm{c}}{\mathrm{2}}}\mathrm{e}^{−\frac{\mathrm{y}}{\mathrm{2}}} =\mathrm{w}\Rightarrow\mathrm{dw}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{w} \\ $$$$\int\frac{\mathrm{1}}{−\mathrm{2}\sqrt{\mathrm{c}}}.\frac{\mathrm{dw}}{\:\sqrt{\mathrm{1}+\mathrm{w}^{\mathrm{2}} }}=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{c}}}\mathrm{argsh}\left(\mathrm{w}\right)=−\frac{\mathrm{argsh}\left(\frac{\sqrt{\mathrm{c}}}{\:\sqrt{\mathrm{2}}}\mathrm{e}^{−\frac{\mathrm{y}}{\mathrm{2}}} \right)}{\mathrm{2}\sqrt{\mathrm{c}}} \\ $$$$\mathrm{if}\:\mathrm{c}\leqslant\mathrm{0} \\ $$$$\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}=\mathrm{arcsin}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\int\frac{\mathrm{e}^{−\frac{\mathrm{y}}{\mathrm{2}}} }{\:\sqrt{\mathrm{2}}\sqrt{\mathrm{1}+\frac{\mathrm{c}}{\mathrm{2}}\mathrm{e}^{−\mathrm{y}} }} \\ $$$$\mathrm{w}=\sqrt{−\frac{\mathrm{c}}{\mathrm{2}}}\mathrm{e}^{−\frac{\mathrm{y}}{\mathrm{2}}} \\ $$$$\int\frac{\mathrm{dw}}{−\mathrm{2}\sqrt{−\mathrm{c}}\left(\sqrt{\mathrm{1}−\mathrm{w}^{\mathrm{2}} }\right)}=−\frac{\mathrm{arcsin}\left(\mathrm{w}\right)}{\mathrm{2}\sqrt{−\mathrm{c}}}=−\frac{\mathrm{arcsin}\left(\sqrt{\frac{−\mathrm{c}}{\mathrm{2}}}\mathrm{e}^{\frac{−\mathrm{y}}{\mathrm{2}}} \right)}{\mathrm{2}\sqrt{−\mathrm{c}}} \\ $$$$\mathrm{c}\geqslant\mathrm{0}\Rightarrow−\frac{\mathrm{argsh}\left(\sqrt{\frac{\mathrm{c}}{\mathrm{2}}}.\mathrm{e}^{\frac{−\mathrm{y}}{\mathrm{2}}} \right)}{\mathrm{2}\sqrt{\mathrm{c}}}=\mathrm{x}+\mathrm{b} \\ $$$$\Rightarrow\mathrm{argsh}\left(\sqrt{\frac{\mathrm{c}}{\mathrm{2}}}\mathrm{e}^{\frac{−\mathrm{y}}{\mathrm{2}}} \right)=−\mathrm{2}\sqrt{\mathrm{c}}\left(\mathrm{x}+\mathrm{b}\right) \\ $$$$\Rightarrow\mathrm{y}=−\mathrm{2ln}\left\{\sqrt{\frac{\mathrm{2}}{\mathrm{c}}}.\mathrm{sh}\left(−\mathrm{2}\sqrt{\mathrm{c}}\left(\mathrm{x}+\mathrm{b}\right)\right)\right\} \\ $$$$−\mathrm{2}\sqrt{\mathrm{c}}\left(\mathrm{x}+\mathrm{b}\right)\geqslant\mathrm{0}\Rightarrow\mathrm{x}\geqslant−\mathrm{b} \\ $$$$\mathrm{c}\leqslant\mathrm{0} \\ $$$$\mathrm{y}=−\mathrm{2ln}\left\{\frac{\mathrm{2}}{\:\sqrt{−\mathrm{c}}}\left(\mathrm{sin}\left(−\mathrm{2}\sqrt{−\mathrm{c}}\left(\mathrm{x}+\mathrm{b}\right)\right).\right\}\right. \\ $$$$\mathrm{2k}\pi<−\mathrm{2}\sqrt{−\mathrm{c}}\left(\mathrm{x}+\mathrm{b}\right)<\left(\mathrm{2k}+\mathrm{1}\right)\pi \\ $$$$\mathrm{because}\:\mathrm{ln}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{defind}\:\mathrm{in}\:\mathrm{x}>\mathrm{0} \\ $$$$\left.\Rightarrow\:\:\:\:\:\:\:\:\:\:\mathrm{x}\in\right]\frac{\mathrm{2k}+\mathrm{1}}{−\mathrm{2}\sqrt{−\mathrm{c}}}\pi_{} −\mathrm{b},\frac{\mathrm{2k}\pi}{−\mathrm{2}\sqrt{−\mathrm{c}}}−\mathrm{b}\left[\:\mathrm{for}\:\mathrm{a}\:\mathrm{given}\:\mathrm{integer}\:\mathrm{k}\right. \\ $$$$ \\ $$

Commented by oyemi kemewari last updated on 06/Nov/19

thanks so much

Commented by mind is power last updated on 06/Nov/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$

Commented by MJS last updated on 06/Nov/19

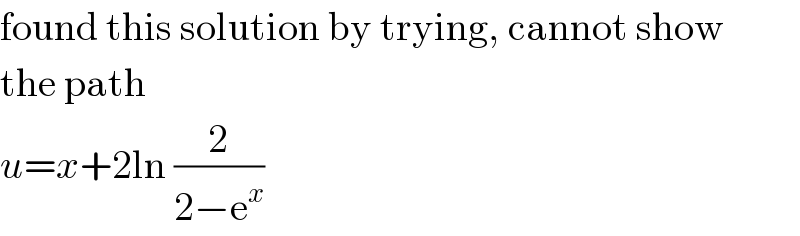
found this solution by trying, cannot show the path u=x+2ln (2/(2−e^x ))

$$\mathrm{found}\:\mathrm{this}\:\mathrm{solution}\:\mathrm{by}\:\mathrm{trying},\:\mathrm{cannot}\:\mathrm{show} \\ $$$$\mathrm{the}\:\mathrm{path} \\ $$$${u}={x}+\mathrm{2ln}\:\frac{\mathrm{2}}{\mathrm{2}−\mathrm{e}^{{x}} } \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply