Menu Close

y-ln-3x-2-x-solve-y-6-x-

Tinku Tara 0 Comments
Pin




Question Number 72044 by 20190927 last updated on 23/Oct/19
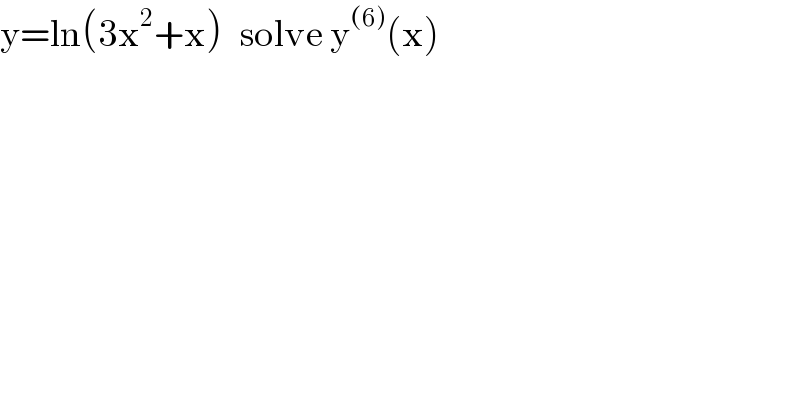
y=ln(3x^2 +x) solve y^((6)) (x)
$$\mathrm{y}=\mathrm{ln}\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{x}\right)\:\:\:\mathrm{solve}\:\mathrm{y}^{\left(\mathrm{6}\right)} \left(\mathrm{x}\right) \\ $$
Commented by mathmax by abdo last updated on 24/Oct/19
we have y^′ (x)=((6x+1)/(3x^2 +x)) =((6x+1)/(x(3x+1))) =(a/x) +(b/(3x+1)) a=1 and b=((6(−(1/3))+1)/((−(1/3)))) =(−3)(−1) =3 ⇒y^′ (x)=(1/x) +(3/(3x+1)) =(1/x) +(1/(x+(1/3))) ⇒y^((6)) (x)=(y^′ (x))^((5)) =((1/x) +(1/(x+(1/3))))^((5)) =((1/x))^((5)) +((1/(x +3^(−1) )))^((5)) =(((−1)^5 5!)/x^6 ) +(((−1)^5 5!)/((x+3^(−1) )^6 )) ⇒ y^((6)) (x)=−5!{(1/x^6 ) +(1/((x+3^(−1) )^6 ))} .
$${we}\:{have}\:{y}^{'} \left({x}\right)=\frac{\mathrm{6}{x}+\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} \:+{x}}\:=\frac{\mathrm{6}{x}+\mathrm{1}}{{x}\left(\mathrm{3}{x}+\mathrm{1}\right)}\:=\frac{{a}}{{x}}\:+\frac{{b}}{\mathrm{3}{x}+\mathrm{1}} \\ $$$${a}=\mathrm{1}\:\:{and}\:{b}=\frac{\mathrm{6}\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)+\mathrm{1}}{\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)}\:=\left(−\mathrm{3}\right)\left(−\mathrm{1}\right)\:=\mathrm{3}\:\Rightarrow{y}^{'} \left({x}\right)=\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{3}}{\mathrm{3}{x}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{\mathrm{3}}}\:\Rightarrow{y}^{\left(\mathrm{6}\right)} \left({x}\right)=\left({y}^{'} \left({x}\right)\right)^{\left(\mathrm{5}\right)} =\left(\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{\mathrm{3}}}\right)^{\left(\mathrm{5}\right)} \\ $$$$=\left(\frac{\mathrm{1}}{{x}}\right)^{\left(\mathrm{5}\right)} \:+\left(\frac{\mathrm{1}}{{x}\:+\mathrm{3}^{−\mathrm{1}} }\right)^{\left(\mathrm{5}\right)} =\frac{\left(−\mathrm{1}\right)^{\mathrm{5}} \mathrm{5}!}{{x}^{\mathrm{6}} }\:+\frac{\left(−\mathrm{1}\right)^{\mathrm{5}} \mathrm{5}!}{\left({x}+\mathrm{3}^{−\mathrm{1}} \right)^{\mathrm{6}} }\:\Rightarrow \\ $$$${y}^{\left(\mathrm{6}\right)} \left({x}\right)=−\mathrm{5}!\left\{\frac{\mathrm{1}}{{x}^{\mathrm{6}} }\:+\frac{\mathrm{1}}{\left({x}+\mathrm{3}^{−\mathrm{1}} \right)^{\mathrm{6}} }\right\}\:. \\ $$
Commented by mathmax by abdo last updated on 25/Oct/19
you are welcome
$${you}\:{are}\:{welcome} \\ $$
Commented by 20190927 last updated on 25/Oct/19
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Joel578 last updated on 24/Oct/19
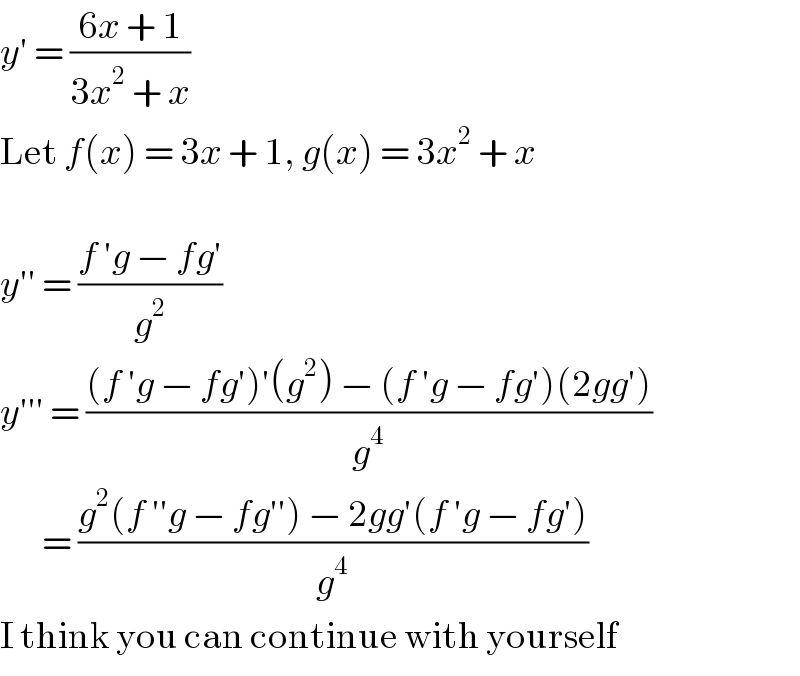
y′ = ((6x + 1)/(3x^2 + x)) Let f(x) = 3x + 1, g(x) = 3x^2 + x y′′ = ((f ′g − fg′)/g^2 ) y′′′ = (((f ′g − fg′)′(g^2 ) − (f ′g − fg′)(2gg′))/g^4 ) = ((g^2 (f ′′g − fg′′) − 2gg′(f ′g − fg′))/g^4 ) I think you can continue with yourself
$${y}'\:=\:\frac{\mathrm{6}{x}\:+\:\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} \:+\:{x}} \\ $$$$\mathrm{Let}\:{f}\left({x}\right)\:=\:\mathrm{3}{x}\:+\:\mathrm{1},\:{g}\left({x}\right)\:=\:\mathrm{3}{x}^{\mathrm{2}} \:+\:{x} \\ $$$$ \\ $$$${y}''\:=\:\frac{{f}\:'{g}\:−\:{fg}'}{{g}^{\mathrm{2}} } \\ $$$${y}'''\:=\:\frac{\left({f}\:'{g}\:−\:{fg}'\right)'\left({g}^{\mathrm{2}} \right)\:−\:\left({f}\:'{g}\:−\:{fg}'\right)\left(\mathrm{2}{gg}'\right)}{{g}^{\mathrm{4}} } \\ $$$$\:\:\:\:\:\:\:=\:\frac{{g}^{\mathrm{2}} \left({f}\:''{g}\:−\:{fg}''\right)\:−\:\mathrm{2}{gg}'\left({f}\:'{g}\:−\:{fg}'\right)}{{g}^{\mathrm{4}} } \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{you}\:\mathrm{can}\:\mathrm{continue}\:\mathrm{with}\:\mathrm{yourself} \\ $$
Commented by 20190927 last updated on 25/Oct/19
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *