Question Number 137667 by aurpeyz last updated on 05/Apr/21
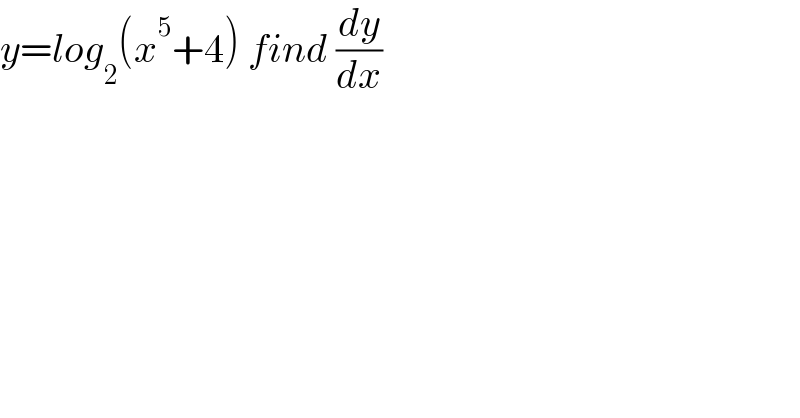
$${y}={log}_{\mathrm{2}} \left({x}^{\mathrm{5}} +\mathrm{4}\right)\:{find}\:\frac{{dy}}{{dx}} \\ $$
Answered by Dwaipayan Shikari last updated on 05/Apr/21
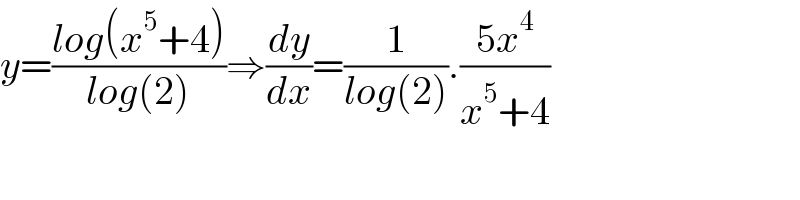
$${y}=\frac{{log}\left({x}^{\mathrm{5}} +\mathrm{4}\right)}{{log}\left(\mathrm{2}\right)}\Rightarrow\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{{log}\left(\mathrm{2}\right)}.\frac{\mathrm{5}{x}^{\mathrm{4}} }{{x}^{\mathrm{5}} +\mathrm{4}} \\ $$
