Question Number 3930 by Filup last updated on 25/Dec/15

$${y}=\frac{\mathrm{log}_{{e}} \left(\frac{{x}}{{m}}−{sa}\right)}{{r}^{\mathrm{2}} } \\ $$$${yr}^{\mathrm{2}} =\mathrm{log}_{\mathrm{e}} \left(\frac{{x}}{{m}}−{sa}\right) \\ $$$${e}^{{yr}^{\mathrm{2}} } =\frac{{x}}{{m}}−{sa} \\ $$$${me}^{{rry}} ={x}−{mas} \\ $$$$ \\ $$$$\mathrm{Merry}\:\mathrm{christmas}\:\mathrm{everyone}! \\ $$$$\mathrm{Let}\:\mathrm{our}\:\mathrm{venture}\:\mathrm{for}\:\mathrm{knowledge}\:\mathrm{continue} \\ $$$$\mathrm{through}\:\mathrm{to}\:\mathrm{the}\:\mathrm{new}\:\mathrm{year}! \\ $$
Commented by Yozzii last updated on 25/Dec/15

$${Same}\:{to}\:{you}!\: \\ $$
Commented by RasheedSindhi last updated on 25/Dec/15
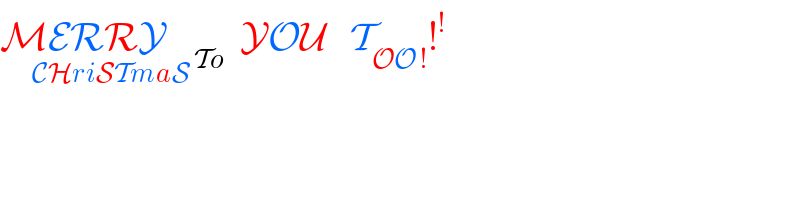
$$\underset{\mathcal{CH}{ri}\mathcal{ST}{ma}\mathcal{S}} {\mathcal{MERRY}_{\:\:\:\:\:\:\:\mathcal{T}{o}} }\:\:\mathcal{YOU}\:\:\:\mathcal{T}_{\mathcal{OO}\:!} !^{!} \\ $$
Commented by prakash jain last updated on 25/Dec/15
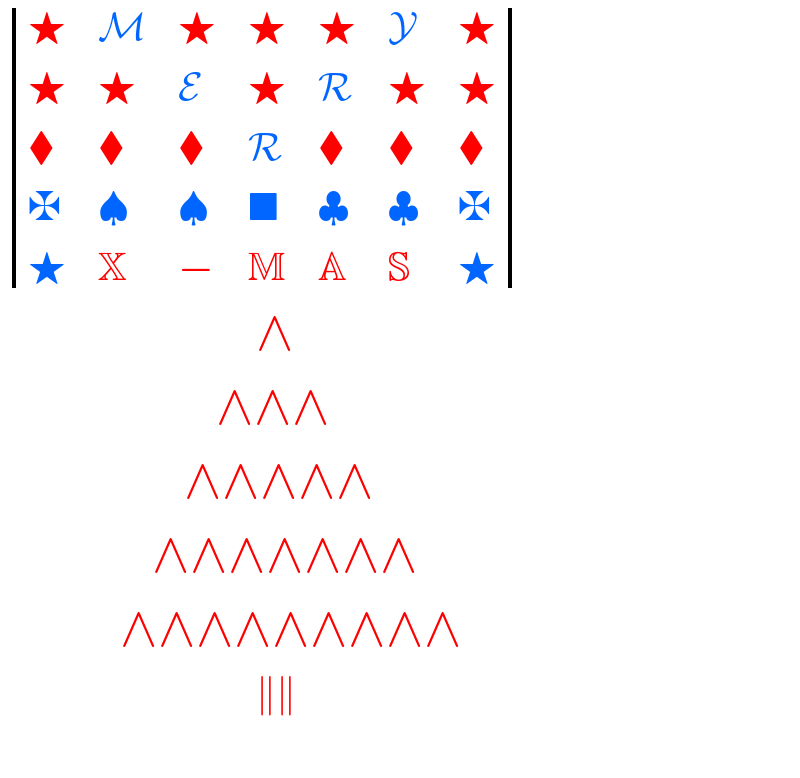
$$\begin{vmatrix}{\bigstar}&{\mathcal{M}}&{\bigstar}&{\bigstar}&{\bigstar}&{\mathcal{Y}}&{\bigstar}\\{\bigstar}&{\bigstar}&{\mathcal{E}}&{\bigstar}&{\mathcal{R}}&{\bigstar}&{\bigstar}\\{\blacklozenge}&{\blacklozenge}&{\blacklozenge}&{\mathcal{R}}&{\blacklozenge}&{\blacklozenge}&{\blacklozenge}\\{\maltese}&{\spadesuit}&{\spadesuit}&{\blacksquare}&{\clubsuit}&{\clubsuit}&{\maltese}\\{\bigstar}&{\mathbb{X}}&{−}&{\mathbb{M}}&{\mathbb{A}}&{\mathbb{S}}&{\bigstar}\end{vmatrix}\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\wedge \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\wedge\wedge\wedge \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\wedge\wedge\wedge\wedge\wedge \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\wedge\wedge\wedge\wedge\wedge\wedge\wedge \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\wedge\wedge\wedge\wedge\wedge\wedge\wedge\wedge\wedge \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\parallel\parallel \\ $$$$ \\ $$
