Question Number 10956 by Joel576 last updated on 04/Mar/17
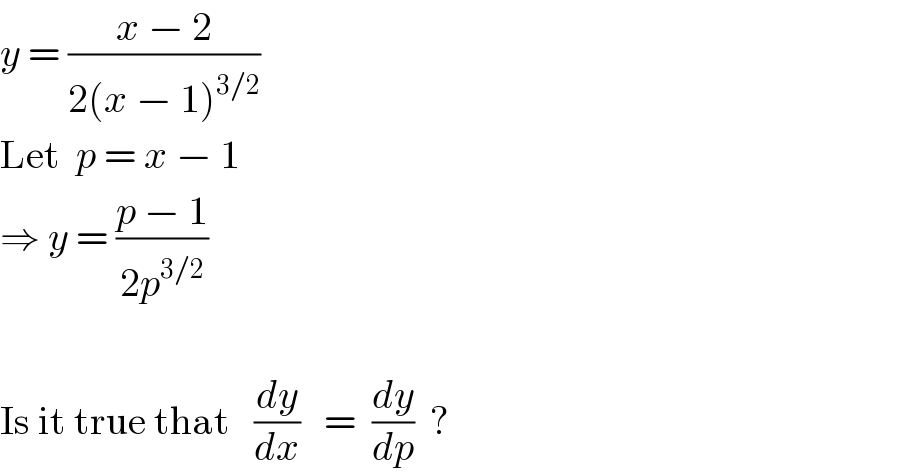
$${y}\:=\:\frac{{x}\:−\:\mathrm{2}}{\mathrm{2}\left({x}\:−\:\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} } \\ $$$$\mathrm{Let}\:\:{p}\:=\:{x}\:−\:\mathrm{1} \\ $$$$\Rightarrow\:{y}\:=\:\frac{{p}\:−\:\mathrm{1}}{\mathrm{2}{p}^{\mathrm{3}/\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{Is}\:\mathrm{it}\:\mathrm{true}\:\mathrm{that}\:\:\:\frac{{dy}}{{dx}}\:\:\:=\:\:\frac{{dy}}{{dp}}\:\:? \\ $$
Commented by FilupS last updated on 04/Mar/17

$$\mathrm{if}\:{p}\:\mathrm{is}\:\mathrm{direct}\:\mathrm{substitution} \\ $$$${f}\left({x}\right)={f}\left({p}\right) \\ $$$$\therefore{f}\:'\left({x}\right)={f}\:'\left({p}\right) \\ $$
Commented by Joel576 last updated on 04/Mar/17
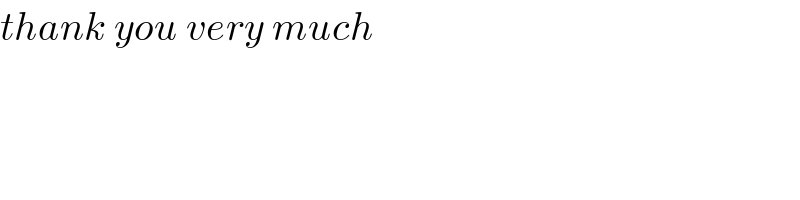
$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by FilupS last updated on 04/Mar/17
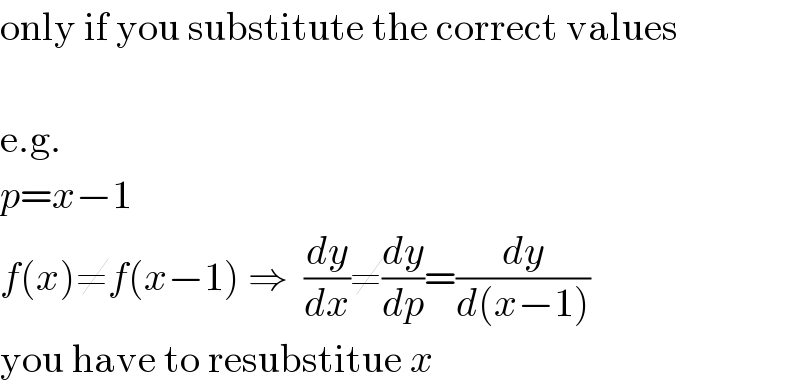
$$\mathrm{only}\:\mathrm{if}\:\mathrm{you}\:\mathrm{substitute}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{values} \\ $$$$\: \\ $$$$\mathrm{e}.\mathrm{g}. \\ $$$${p}={x}−\mathrm{1} \\ $$$${f}\left({x}\right)\neq{f}\left({x}−\mathrm{1}\right)\:\Rightarrow\:\:\frac{{dy}}{{dx}}\neq\frac{{dy}}{{dp}}=\frac{{dy}}{{d}\left({x}−\mathrm{1}\right)} \\ $$$$\mathrm{you}\:\mathrm{have}\:\mathrm{to}\:\mathrm{resubstitue}\:{x} \\ $$
Commented by FilupS last updated on 04/Mar/17

$$\mathrm{if}\:{x}={g}\left({u}\right) \\ $$$$\mathrm{and}\:{u}={h}\left({x}\right) \\ $$$$\: \\ $$$${y}={f}\left({x}\right) \\ $$$${y}={g}\left({h}\left({x}\right)\right) \\ $$$$\therefore\:\frac{{dy}}{{dx}}=\frac{{dy}}{{du}}×\frac{{du}}{{dx}} \\ $$
