Question Number 12562 by @ANTARES_VY last updated on 25/Apr/17

$$\boldsymbol{\mathrm{y}}=−\frac{\boldsymbol{\mathrm{x}}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{3}\boldsymbol{\mathrm{x}} \\ $$$$\boldsymbol{\mathrm{maximum}}−\boldsymbol{\mathrm{minimum}}=? \\ $$
Commented by sandy_suhendra last updated on 25/Apr/17

$$\mathrm{do}\:\mathrm{you}\:\mathrm{mean}\:''\mathrm{max}\:\mathrm{stationary}''\:\mathrm{and}\:''\mathrm{min}\:\mathrm{stationary}''\:? \\ $$
Answered by mrW1 last updated on 25/Apr/17
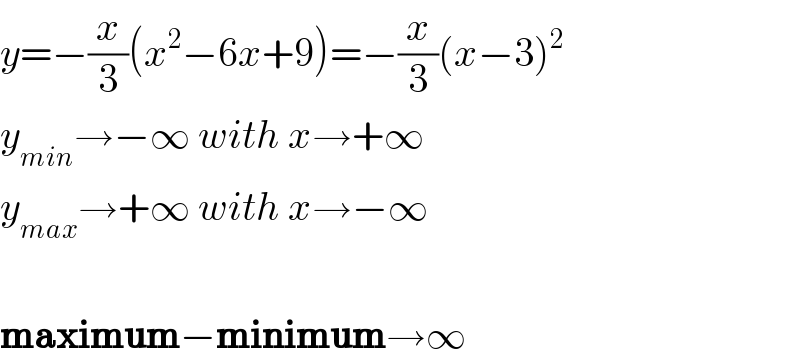
$${y}=−\frac{{x}}{\mathrm{3}}\left({x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9}\right)=−\frac{{x}}{\mathrm{3}}\left({x}−\mathrm{3}\right)^{\mathrm{2}} \\ $$$${y}_{{min}} \rightarrow−\infty\:{with}\:{x}\rightarrow+\infty \\ $$$${y}_{{max}} \rightarrow+\infty\:{with}\:{x}\rightarrow−\infty \\ $$$$ \\ $$$$\boldsymbol{\mathrm{maximum}}−\boldsymbol{\mathrm{minimum}}\rightarrow\infty \\ $$
