y-y-8cos-t-y-0-1-y-0-1-

Question Number 1056 by 123456 last updated on 25/May/15

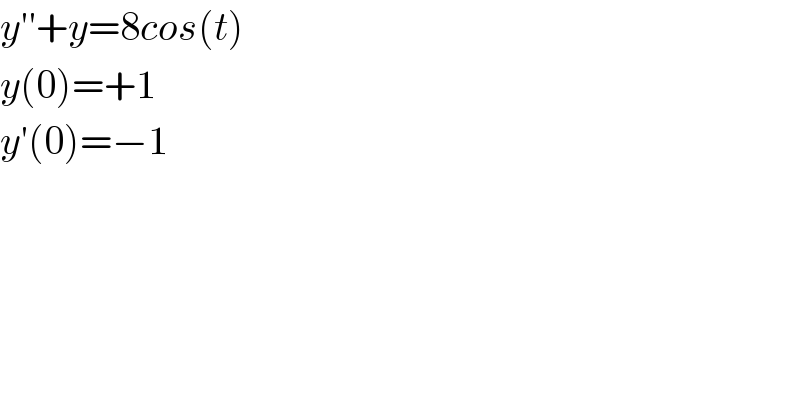
$${y}''+{y}=\mathrm{8}{cos}\left({t}\right) \\ $$$${y}\left(\mathrm{0}\right)=+\mathrm{1} \\ $$$${y}'\left(\mathrm{0}\right)=−\mathrm{1} \\ $$

Commented by prakash jain last updated on 26/May/15

characterstic equation r^2 +1=0 y_h =c_1 cos t+c_2 sin t

$$\mathrm{characterstic}\:\mathrm{equation} \\ $$$${r}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${y}_{{h}} ={c}_{\mathrm{1}} \mathrm{cos}\:{t}+{c}_{\mathrm{2}} \mathrm{sin}\:{t} \\ $$

Answered by prakash jain last updated on 26/May/15

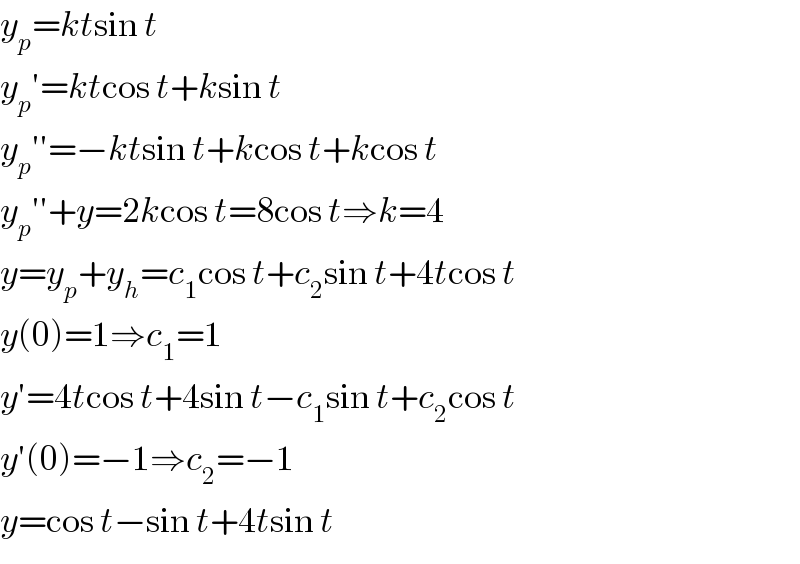
y_p =ktsin t y_p ′=ktcos t+ksin t y_p ′′=−ktsin t+kcos t+kcos t y_p ′′+y=2kcos t=8cos t⇒k=4 y=y_p +y_h =c_1 cos t+c_2 sin t+4tcos t y(0)=1⇒c_1 =1 y′=4tcos t+4sin t−c_1 sin t+c_2 cos t y′(0)=−1⇒c_2 =−1 y=cos t−sin t+4tsin t

$${y}_{{p}} ={kt}\mathrm{sin}\:{t} \\ $$$${y}_{{p}} '={kt}\mathrm{cos}\:{t}+{k}\mathrm{sin}\:{t} \\ $$$${y}_{{p}} ''=−{kt}\mathrm{sin}\:{t}+{k}\mathrm{cos}\:{t}+{k}\mathrm{cos}\:{t} \\ $$$${y}_{{p}} ''+{y}=\mathrm{2}{k}\mathrm{cos}\:{t}=\mathrm{8cos}\:{t}\Rightarrow{k}=\mathrm{4} \\ $$$${y}={y}_{{p}} +{y}_{{h}} ={c}_{\mathrm{1}} \mathrm{cos}\:{t}+{c}_{\mathrm{2}} \mathrm{sin}\:{t}+\mathrm{4}{t}\mathrm{cos}\:{t} \\ $$$${y}\left(\mathrm{0}\right)=\mathrm{1}\Rightarrow{c}_{\mathrm{1}} =\mathrm{1} \\ $$$${y}'=\mathrm{4}{t}\mathrm{cos}\:{t}+\mathrm{4sin}\:{t}−{c}_{\mathrm{1}} \mathrm{sin}\:{t}+{c}_{\mathrm{2}} \mathrm{cos}\:{t} \\ $$$${y}'\left(\mathrm{0}\right)=−\mathrm{1}\Rightarrow{c}_{\mathrm{2}} =−\mathrm{1} \\ $$$${y}=\mathrm{cos}\:{t}−\mathrm{sin}\:{t}+\mathrm{4}{t}\mathrm{sin}\:{t} \\ $$

Facebook Tweet Pin

y-y-8cos-t-y-0-1-y-0-1-

Leave a Reply Cancel reply